Question
The area bounded by the curve $$y = {\sin ^{ - 1}}x$$ and the line $$x = 0,\,\left| y \right| = \frac{\pi }{2}$$ is :
A.
$$1$$
B.
$$2$$
C.
$$\pi $$
D.
$$2\pi $$
Answer :
$$2$$
Solution :
The required area is shown by shaded portion in the figure.
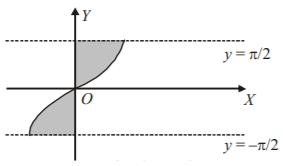
The required area is $$A = \int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left| {\sin \,y} \right|dy = 2\int\limits_0^{\frac{\pi }{2}} {\sin \,y\,dy} = 2} $$
The required area is shown by shaded portion in the figure.

The required area is $$A = \int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left| {\sin \,y} \right|dy = 2\int\limits_0^{\frac{\pi }{2}} {\sin \,y\,dy} = 2} $$