Question
The area between the parabolas $${x^2} = \frac{y}{4}$$ and $${x^2} = 9y$$ and the straight line $$y = 2$$ is:
A.
$$20\sqrt 2 $$
B.
$$\frac{{10\sqrt 2 }}{3}$$
C.
$$\frac{{20\sqrt 2 }}{3}$$
D.
$$10\sqrt 2 $$
Answer :
$$\frac{{20\sqrt 2 }}{3}$$
Solution :
Given curves $${x^2} = \frac{y}{4}$$ and $${x^2} = 9y$$ are the parabolas whose equations can be written as $$y = 4{x^2}$$ and $$y = \frac{1}{9}{x^2}.$$
Also, given $$y = 2.$$
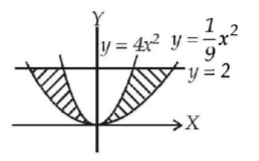
Now, shaded portion shows the required area which is symmetric.
$$\eqalign{ & \therefore {\text{Area}} = 2\int\limits_0^2 {\left( {\sqrt {9y} - \sqrt {\frac{y}{4}} } \right)dy} \cr & {\text{Area}} = 2\int\limits_0^2 {\left( {3\sqrt y - \sqrt {\frac{y}{2}} } \right)dy} \cr & = 2\left[ {\frac{2}{3} \times 3.{y^{\frac{3}{2}}} - \frac{1}{2} \times \frac{2}{3}.{y^{\frac{3}{2}}}} \right]_0^2 \cr & = 2\left[ {2{y^{\frac{3}{2}}} - \frac{1}{3}{y^{\frac{3}{2}}}} \right]_0^2 \cr & = \left. {2 \times \frac{5}{3}{y^{\frac{3}{2}}}} \right|_0^2 \cr & = 2.\frac{5}{3}.2\sqrt 2 \cr & = \frac{{20\sqrt 2 }}{3} \cr} $$
Given curves $${x^2} = \frac{y}{4}$$ and $${x^2} = 9y$$ are the parabolas whose equations can be written as $$y = 4{x^2}$$ and $$y = \frac{1}{9}{x^2}.$$
Also, given $$y = 2.$$

Now, shaded portion shows the required area which is symmetric.
$$\eqalign{ & \therefore {\text{Area}} = 2\int\limits_0^2 {\left( {\sqrt {9y} - \sqrt {\frac{y}{4}} } \right)dy} \cr & {\text{Area}} = 2\int\limits_0^2 {\left( {3\sqrt y - \sqrt {\frac{y}{2}} } \right)dy} \cr & = 2\left[ {\frac{2}{3} \times 3.{y^{\frac{3}{2}}} - \frac{1}{2} \times \frac{2}{3}.{y^{\frac{3}{2}}}} \right]_0^2 \cr & = 2\left[ {2{y^{\frac{3}{2}}} - \frac{1}{3}{y^{\frac{3}{2}}}} \right]_0^2 \cr & = \left. {2 \times \frac{5}{3}{y^{\frac{3}{2}}}} \right|_0^2 \cr & = 2.\frac{5}{3}.2\sqrt 2 \cr & = \frac{{20\sqrt 2 }}{3} \cr} $$