Question
‘The angle between a pair of tangents drawn from a point $$P$$ to the circle $${x^2} + {y^2} + 4x - 6y + 9\,{\sin ^2}\alpha + 13\,{\cos ^2}\alpha = 0$$ is $$2\alpha .$$ The equation of the locus of the point $$P$$ is-
A.
$${x^2} + {y^2} + 4x - 6y + 4 = 0$$
B.
$${x^2} + {y^2} + 4x - 6y - 9 = 0$$
C.
$${x^2} + {y^2} + 4x - 6y - 4 = 0$$
D.
$${x^2} + {y^2} + 4x - 6y + 9 = 0$$
Answer :
$${x^2} + {y^2} + 4x - 6y + 9 = 0$$
Solution :
Centre of the circle
$${x^2} + {y^2} + 4x - 6y + 9\,{\sin ^2}\alpha + 13\,{\cos ^2}\alpha = 0$$
is $$C\left( { - 2,\,3} \right)$$ and its radius is
$$\eqalign{ & \sqrt {{2^2} + {{\left( { - 3} \right)}^2} - 9\,{{\sin }^2}\alpha + 13\,{{\cos }^2}\alpha } \cr & = \sqrt {4 + 9 - 9\,{{\sin }^2}\alpha + 13\,{{\cos }^2}\alpha } \cr & = 2\,\sin \,\alpha \cr} $$
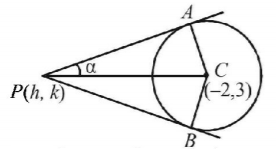
Let $$P\left( {h,\,k} \right)$$ be any point on the locus. The $$\angle APC = \alpha $$
Also $$\angle PAC = \frac{\pi }{2}$$
That is, triangle $$APC$$ is a right triangle.
Thus, $$\sin \,\alpha = \frac{{AC}}{{PC}} = \frac{{2\,\sin \,\alpha }}{{\sqrt {{{\left( {h + 2} \right)}^2} + {{\left( {k - 3} \right)}^2}} }}$$
$$\eqalign{ & \Rightarrow \sqrt {{{\left( {h + 2} \right)}^2} + {{\left( {k - 3} \right)}^2}} = 2 \cr & \Rightarrow {\left( {h + 2} \right)^2} + {\left( {k - 3} \right)^2} = 4 \cr & {\text{or}}\,\,{h^2} + {k^2} + 4h - 6k + 9 = 0 \cr} $$
Thus required equation of the locus is $${x^2} + {y^2} + 4x - 6y + 9 = 0$$
Centre of the circle
$${x^2} + {y^2} + 4x - 6y + 9\,{\sin ^2}\alpha + 13\,{\cos ^2}\alpha = 0$$
is $$C\left( { - 2,\,3} \right)$$ and its radius is
$$\eqalign{ & \sqrt {{2^2} + {{\left( { - 3} \right)}^2} - 9\,{{\sin }^2}\alpha + 13\,{{\cos }^2}\alpha } \cr & = \sqrt {4 + 9 - 9\,{{\sin }^2}\alpha + 13\,{{\cos }^2}\alpha } \cr & = 2\,\sin \,\alpha \cr} $$

Let $$P\left( {h,\,k} \right)$$ be any point on the locus. The $$\angle APC = \alpha $$
Also $$\angle PAC = \frac{\pi }{2}$$
That is, triangle $$APC$$ is a right triangle.
Thus, $$\sin \,\alpha = \frac{{AC}}{{PC}} = \frac{{2\,\sin \,\alpha }}{{\sqrt {{{\left( {h + 2} \right)}^2} + {{\left( {k - 3} \right)}^2}} }}$$
$$\eqalign{ & \Rightarrow \sqrt {{{\left( {h + 2} \right)}^2} + {{\left( {k - 3} \right)}^2}} = 2 \cr & \Rightarrow {\left( {h + 2} \right)^2} + {\left( {k - 3} \right)^2} = 4 \cr & {\text{or}}\,\,{h^2} + {k^2} + 4h - 6k + 9 = 0 \cr} $$
Thus required equation of the locus is $${x^2} + {y^2} + 4x - 6y + 9 = 0$$