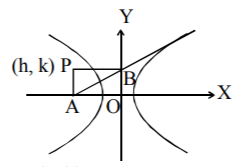
Tangents at any point on the hyperbola $$\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$$   cut the axes at $$A$$ and $$B$$ respectively. If the rectangle $$OAPB$$   (where $$O$$ is the origin) is completed, then locus of point $$P$$ is given by :

Solution :
Equation of the tangent at the point $$'\theta '$$ is $$\frac{{x\,\sec \,\theta }}{a} - \frac{{y\,\tan \,\theta }}{b} = 1$$
$$\eqalign{ & \Rightarrow A{\text{ is}}\left( {a\,\cos \,\theta ,\,0} \right){\text{and }}B{\text{ is}}\left( {0,\, - b\,\cot \,\theta } \right) \cr & {\text{Let }}P{\text{ be}}\left( {h,\,k} \right) \Rightarrow h = a\,\cos \,\theta ,\,k = - b\,\cot \,\theta \cr & \Rightarrow \frac{k}{h} = - \frac{b}{{a\,\sin \,\theta }} \cr & \Rightarrow \sin \,\theta = - \frac{{bh}}{{ak}}{\text{ and cos}}\,\theta = \frac{h}{a} \cr} $$

Square and add,
$$\eqalign{ & \Rightarrow \frac{{{b^2}{h^2}}}{{{a^2}{k^2}}} + \frac{{{h^2}}}{{{a^2}}} = 1 \cr & \Rightarrow \frac{{{b^2}}}{{{k^2}}} + 1 = \frac{{{a^2}}}{{{h^2}}} \cr & \Rightarrow \frac{{{a^2}}}{{{h^2}}} - \frac{{{b^2}}}{{{k^2}}} = 1 \cr} $$
Hence, locus of $$P$$ is $$\frac{{{a^2}}}{{{x^2}}} - \frac{{{b^2}}}{{{y^2}}} = 1$$