Question
Suppose $${z_1},{z_2},{z_3}$$ are the vertices of an equilateral triangle inscribed in the circle $$\left| z \right| = 2.$$ If $${z_1} = 1 + \sqrt {3}i $$ and $${z_1},{z_2},{z_3}$$ are in the clockwise sense then
A.
$${z_2} = 1 - \sqrt {3}i ,{z_3} = - 2$$
B.
$${z_2} = 2,{z_3} = 1 - \sqrt {3}i $$
C.
$${z_2} = - 1 + \sqrt {3}i ,{z_3} = - 2$$
D.
None of these
Answer :
$${z_2} = 1 - \sqrt {3}i ,{z_3} = - 2$$
Solution :
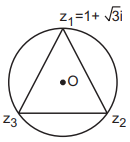
$$\eqalign{ & {\text{amp}}\,{z_1} = {\text{amp}}\left( {1 + \sqrt {3}i } \right) = {\tan ^{ - 1}}\sqrt 3 = \frac{\pi }{3}. \cr & {\text{amp}}\,{z_2} = \frac{\pi }{3} - \frac{{2\pi }}{3} = - \frac{\pi }{3}\,\,{\text{and }}\left| {{z_2}} \right| = 2 \cr & \therefore \,\,{z_2} = 2\left\{ {\cos \left( { - \frac{\pi }{3}} \right) + i\sin \left( { - \frac{\pi }{3}} \right)} \right\}. \cr & {\text{amp }}{z_3} = \frac{\pi }{3} + \frac{{2\pi }}{3} = \pi \,\,{\text{and }}\left| {{z_3}} \right| = 2 \cr & \therefore \,\,{z_3} = 2\left\{ {\cos \pi + i\sin \pi } \right\}. \cr} $$

$$\eqalign{ & {\text{amp}}\,{z_1} = {\text{amp}}\left( {1 + \sqrt {3}i } \right) = {\tan ^{ - 1}}\sqrt 3 = \frac{\pi }{3}. \cr & {\text{amp}}\,{z_2} = \frac{\pi }{3} - \frac{{2\pi }}{3} = - \frac{\pi }{3}\,\,{\text{and }}\left| {{z_2}} \right| = 2 \cr & \therefore \,\,{z_2} = 2\left\{ {\cos \left( { - \frac{\pi }{3}} \right) + i\sin \left( { - \frac{\pi }{3}} \right)} \right\}. \cr & {\text{amp }}{z_3} = \frac{\pi }{3} + \frac{{2\pi }}{3} = \pi \,\,{\text{and }}\left| {{z_3}} \right| = 2 \cr & \therefore \,\,{z_3} = 2\left\{ {\cos \pi + i\sin \pi } \right\}. \cr} $$