81. A projectile is thrown in the upward direction making an angle of $${60^ \circ }$$ with the horizontal direction with a velocity of $$147\,m{s^{ - 1}}.$$ Then the time after which its inclination with the horizontal is $${45^ \circ },$$ is
A
$$15\left( {\sqrt 3 - 1} \right)s$$
B
$$15\left( {\sqrt 3 + 1} \right)s$$
C
$$7.5\left( {\sqrt 3 - 1} \right)s$$
D
$$7.5\left( {\sqrt 3 + 1} \right)s$$
Answer :
$$7.5\left( {\sqrt 3 - 1} \right)s$$
82. The angle which the velocity vector of a projectile thrown with a velocity $$v$$ at an angle $$\theta $$ to the horizontal will make with the horizontal after time $$t$$ of its being thrown up is:
A
$$\theta $$
B
$${\tan ^{ - 1}}\left( {\frac{\theta }{t}} \right)$$
C
$${\tan ^{ - 1}}\left( {\frac{{v\cos \theta }}{{v\sin \theta - gt}}} \right)$$
D
$${\tan ^{ - 1}}\left( {\frac{{v\sin \theta - gt}}{{v\cos \theta }}} \right)$$
Answer :
$${\tan ^{ - 1}}\left( {\frac{{v\sin \theta - gt}}{{v\cos \theta }}} \right)$$
83. The angle between $$A$$ and $$B$$ is $$\theta .$$ The value of the triple product $$A \cdot \left( {B \times A} \right)$$ is
A
$${A^2}B$$
B
zero
C
$${A^2}B\sin \theta $$
D
$${A^2}B\cos \theta $$
Answer :
zero
84.
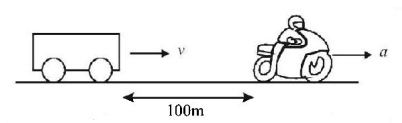
A man travelling in a car with a maximum constant speed of $$20\,m/s$$ watches the friend start off at a distance $$100\,m$$ ahead on a motor cycle with constant acceleration $$'a'.$$ The maximum value of $$'a'$$ for which the man in the car can reach his friend is
A
$$2\,m/{s^2}$$
B
$$1\,m/{s^2}$$
C
$$4\,m/{s^2}$$
D
$$8\,m{s^{ - 2}}$$
Answer :
$$2\,m/{s^2}$$
85. The circular motion of a particle with constant speed is
A
simple harmonic but not periodic
B
periodic and simple harmonic
C
neither periodic nor simple harmonic
D
periodic but not simple harmonic
Answer :
periodic but not simple harmonic
86. The resultant of vectors $${\vec P}$$ and $${\vec Q}$$ is $${\vec R}.$$ On reversing the direction of $${\vec Q},$$ the resultant vector becomes $${\vec S}.$$ Then, correct relation is
A
$${R^2} + {S^2} = 2\left( {{P^2} + {Q^2}} \right).$$
B
$${R^2} + {S^2} = {P^2} + {Q^2}$$
C
$${R^2} + {P^2} = {S^2} + {Q^2}$$
D
$${P^2} + {S^2} = 2\left( {{Q^2} + {R^2}} \right)$$
Answer :
$${R^2} + {S^2} = 2\left( {{P^2} + {Q^2}} \right).$$
87. If a ball is thrown vertically upwards with speed $$u,$$ the distance covered during the last $$t$$ $$\sec$$ of its ascent is
A
$$ut - \frac{1}{2}g{t^2}$$
B
$$\left( {u + gt} \right)t$$
C
$$ut$$
D
$$\frac{1}{2}g{t^2}$$
Answer :
$$\frac{1}{2}g{t^2}$$
88.
The position of a projectile launched from the origin at $$t = 0$$ is given by $$\vec r = \left( {40\hat i + 50\hat j} \right)m$$ at $$t = 2s.$$ If the projectile was launched at an angle $$\theta $$ from the horizontal, then $$\theta $$ is
(take $$g = 10\,m{s^{ - 2}}$$ )
A
$${\tan ^{ - 1}}\frac{2}{3}$$
B
$${\tan ^{ - 1}}\frac{3}{2}$$
C
$${\tan ^{ - 1}}\frac{7}{4}$$
D
$${\tan ^{ - 1}}\frac{4}{5}$$
Answer :
$${\tan ^{ - 1}}\frac{7}{4}$$
89. Two particles $$P$$ and $$Q$$ simultaneously start moving from point $$A$$ with velocities $$15\,m/s$$ and $$20\,m/s$$ respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When $$P$$ overtakes $$Q$$ at $$B$$ then its velocity is $$30\,m/s$$ The velocity of $$Q$$ at point $$B$$ will be
A
$$30\,m/s$$
B
$$5\,m/s$$
C
$$20\,m/s$$
D
$$15\,m/s$$
Answer :
$$5\,m/s$$
90. Two boats $$A$$ and $$B,$$ move away from a buoy anchored at the middle of a river along the mutually perpendicular straight lines : the boat $$A$$ along the river and the boat $$B$$ across the river. Having moved off an equal distance from the buoy the boat returned. What is the ratio of times of motion of boats $$\frac{{{\tau _A}}}{{{\tau _B}}},$$ if the velocity of each boat with respect to water is 1.2 times greater than the stream velocity.`
A
2.3
B
1.8
C
0.5
D
0.2
Answer :
1.8