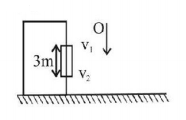
61.
A boat $$B$$ is moving upstream with velocity $$3\,m/s$$ with respect to ground. An observer standing on boat observes that a swimmer $$S$$ is crossing the river perpendicular to the direction of motion of boat. If river flow velocity is $$4\,m/s$$ and swimmer crosses the river of width $$100\,m$$ in $$50\,\sec,$$ then
A
velocity of swimmer w.r.t ground is $$\sqrt {13} \,m/s$$
B
drift of swimmer along river is zero
C
drift of swimmer along river will be $$50\,m$$
D
velocity of swimmer w.r.t ground is $$2\,m/s$$
Answer :
velocity of swimmer w.r.t ground is $$\sqrt {13} \,m/s$$
62. Two bodies $$A$$ (of mass $$1\,kg$$ ) and $$B$$ (of mass $$3\,kg$$ ) are dropped from heights of $$16\,m$$ and $$25\,m,$$ respectively. The ratio of the time taken by them to reach the ground is
A
$$ - \frac{5}{4}$$
B
$$\frac{{12}}{5}$$
C
$$\frac{5}{{12}}$$
D
$$\frac{4}{5}$$
Answer :
$$\frac{4}{5}$$
63. It was calculated that a shell when fired from a gun with a certain velocity and at an angle of elevation $$\frac{{5\pi }}{{36}}\,rad$$ should strike a given target. In actual practice, it was found that a hill just prevented the trajectory. At what angle (rad) of elevation should the gun be fired to hit the target
A
$$\frac{{5\pi }}{{36}}$$
B
$$\frac{{11\pi }}{{36}}$$
C
$$\frac{{7\pi }}{{36}}$$
D
$$\frac{{13\pi }}{{36}}$$
Answer :
$$\frac{{13\pi }}{{36}}$$
64. A particle starting with certain initial velocity and uniform acceleration covers a distance of $$12\,m$$ in first $$3$$ seconds and a distance of $$30\,m$$ in next $$3$$ seconds. The initial velocity of the particle is
A
$$3\,m{s^{ - 1}}$$
B
$$2.5\,m{s^{ - 1}}$$
C
$$2\,m{s^{ - 1}}$$
D
$$1\,m{s^{ - 1}}$$
Answer :
$$1\,m{s^{ - 1}}$$
65. A ball is dropped from the top of a building. The ball takes $$0.5\,s$$ to fall past the $$3m$$ length of a window some distance from the top of the building. If the velocities of the ball at the top and at the bottom of the window are $${v_T}$$ and $${v_B}$$ respectively, then (take $$g = 10\,m/{s^2}$$ )
A
$${v_T} + {v_B} = 12\,m{s^{ - 1}}$$
B
$${v_T} - {v_B} = 4.9\,m{s^{ - 1}}$$
C
$${v_B}{v_T} = 1\,m{s^{ - 1}}$$
D
$$\frac{{{v_B}}}{{{v_T}}} = 1\,m{s^{ - 1}}$$
Answer :
$${v_T} - {v_B} = 4.9\,m{s^{ - 1}}$$
66. A boy can throw a stone up to a maximum height of $$10 \,m.$$ The maximum horizontal distance that the boy can throw the same stone up to will be:
A
$$20\sqrt 2 \,m$$
B
$$10 \,m$$
C
$$10\sqrt 2 \,m$$
D
$$20 \,m$$
Answer :
$$20 \,m$$
67. Two particles are projected with same initial velocities at an angle $${30^ \circ }$$ and $${60^ \circ }$$ with the horizontal. Then,
A
their heights will be equal
B
their ranges will be equal
C
their time of flights will be equal
D
their ranges will be different
Answer :
their ranges will be equal
68. A ball is dropped vertically from a height $$d$$ above the ground. It hits the ground and bounces up vertically to a height $$\frac{d}{2}.$$ Neglecting subsequent motion and air resistance, its velocity $$v$$ varies with the height $$h$$ above the ground as-
A
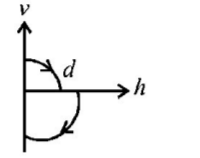

B
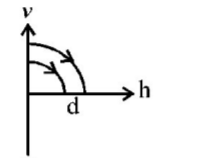

C
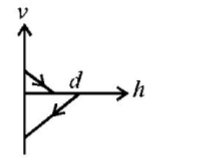

D
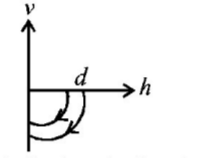

Answer :


69. A boat is moving with a velocity $$3\hat i + 4\hat j$$ with respect to ground. The water in the river is moving with a velocity $$ - 3\hat i - 4\hat j$$ with respect to ground. The relative velocity of the boat with respect to water is
A
$$8\hat j$$
B
$$ - 6\hat i - 8\hat j$$
C
$$6\hat i + 8\hat j$$
D
$$5\sqrt 2 $$
Answer :
$$6\hat i + 8\hat j$$
70.
Two identical discs of same radius $$R$$ are rotating about their axes in opposite directions with the same constant angular speed $$\omega .$$ The discs are in the same horizontal plane. At time $$t=0,$$ the points $$P$$ and $$Q$$ are facing each other as shown in the figure. The relative speed between the two points $$P$$ and $$Q$$ is $${v_r}.$$ In one time period $$\left( T \right)$$ of rotation of the discs, $${v_r}$$ as a function of time is best represented by-

A
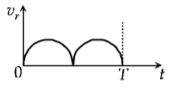

B


C


D


Answer :