11. The co-ordinates of a moving particle at any time $$'t \,'$$ are given by $$x = \alpha {t^3}$$ and $$y = \beta {t^3}.$$ The speed of the particle at time $$'t\,'$$ is given by-
A
$$3t\sqrt {{\alpha ^2} + {\beta ^2}} $$
B
$$3{t^2}\sqrt {{\alpha ^2} + {\beta ^2}} $$
C
$${t^2}\sqrt {{\alpha ^2} + {\beta ^2}} $$
D
$$\sqrt {{\alpha ^2} + {\beta ^2}} $$
Answer :
$$3{t^2}\sqrt {{\alpha ^2} + {\beta ^2}} $$
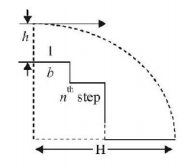
12. A ball rolls off to the top of a staircase with a horizontal velocity $$u\,m/s.$$ If the steps are $$h$$ metre high and $$b$$ metre wide, the ball will hit the edge of the $${n^{th}}$$ step, if
A
$$n = \frac{{2hu}}{{g{b^2}}}$$
B
$$n = \frac{{2h{u^2}}}{{gb}}$$
C
$$n = \frac{{2h{u^2}}}{{g{b^2}}}$$
D
$$n = \frac{{h{u^2}}}{{g{b^2}}}$$
Answer :
$$n = \frac{{2h{u^2}}}{{g{b^2}}}$$
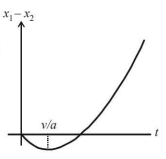
13. A body is at rest at $$x =0.$$ At $$t=0,$$ it starts moving in the positive x-direction with a constant acceleration. At the same instant another body passes through $$x = 0$$ moving in the positive x-direction with a constant speed. The position of the first body is given by $${x_1}\left( t \right)$$ after time $$'t\, ’;$$ and that of the second body by $${x_2}\left( t \right)$$ after the same time interval. Which of the following graphs correctly describes $$\left( {{x_1} - {x_2}} \right)$$ as a function of time $$'t \,'$$ ?
A


B


C
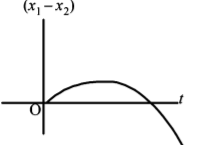

D


Answer :


14.
A particle moves along a straight line such that its displacement at any time $$t$$ is given by $$s = \left( {{t^3} - 6{t^2} + 3t + 4} \right)m$$
The velocity when the acceleration is zero, is
A
$$3\,m{s^{ - 1}}$$
B
$$ - 12\,m{s^{ - 1}}$$
C
$$42\,m{s^{ - 1}}$$
D
$$ - 9\,m{s^{ - 1}}$$
Answer :
$$ - 9\,m{s^{ - 1}}$$
15. A body is thrown vertically upwards. Which one of the following graphs correctly represent the velocity vs time?
A


B
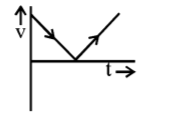

C
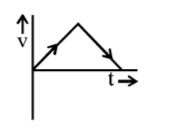

D
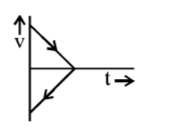

Answer :


16. If a unit vector is represented by $$0.5\hat i + 0.8\hat j + c\hat k,$$ then the value of $$c$$ is
A
$$1$$
B
$$\sqrt {0.8} $$
C
$$\sqrt {0.11} $$
D
$$\sqrt {0.01} $$
Answer :
$$\sqrt {0.11} $$
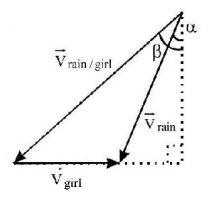
17. Rain, pouring down at an angle $$\alpha $$ with the vertical has a speed of $$10\,m{s^{ - 1}}.$$ A girl runs against the rain with a speed of $$8\,m{s^{ - 1}}$$ and sees that the rain makes an angle $$\beta $$ with the vertical, then relation between $$\alpha $$ and $$\beta $$ is
A
$$\tan \alpha = \frac{{8 + 10\sin \beta }}{{10\cos \beta }}$$
B
$$\tan \beta = \frac{{8 + 10\sin \alpha }}{{10\cos \alpha }}$$
C
$$\tan \alpha = \tan \beta $$
D
$$\tan \alpha = \cot \beta $$
Answer :
$$\tan \beta = \frac{{8 + 10\sin \alpha }}{{10\cos \alpha }}$$
18. A particle moves a distance $$x$$ in time $$t$$ according to equation $$x = {\left( {t + 5} \right)^{ - 1}}.$$ The acceleration of particle is proportional to
A
$${\left( {{\text{velocity}}} \right)^{\frac{3}{2}}}$$
B
$${\left( {{\text{distance}}} \right)^2}$$
C
$${\left( {{\text{distance}}} \right)^{ - 2}}$$
D
$${\left( {{\text{velocity}}} \right)^{\frac{2}{3}}}$$
Answer :
$${\left( {{\text{velocity}}} \right)^{\frac{3}{2}}}$$
19. The acceleration of a particle, starting from rest, varies with time according to the relation $$a = - s{\omega ^2}\sin \omega t.$$ The displacement of this particle at a time $$t$$ will be
A
$$s\sin \omega t$$
B
$$s\,\omega \cos \omega t$$
C
$$s\,\omega \sin \omega t$$
D
$$ - \frac{1}{2}\left( {s\,{\omega ^2}\sin \omega t} \right){t^2}$$
Answer :
$$s\sin \omega t$$
20. The distance time graph of a particle at time $$t$$ makes angles $${45^ \circ }$$ with the time axis. After one second, it makes angle $${60^ \circ }$$ with the time axis. What is the acceleration of the particle?
A
$$\sqrt 3 - 1$$
B
$$\sqrt 3 + 1$$
C
$$\sqrt 3 $$
D
$$1$$
Answer :
$$\sqrt 3 - 1$$