Question
$${L_r},\,{m_r},\,{n_r};\,r = 1,\,2,\,3;$$ are the direction cosines of three mutually perpendicular lines. The direction cosines of the line equally inclined to them are :
A.
$${l_1} + {l_2} + {l_3},\,{m_1} + {m_2} + {m_3},\,{n_1} + {n_2} + {n_3}$$
B.
$$\frac{{{l_1} + {l_2} + {l_3}}}{3},\,\frac{{{m_1} + {m_2} + {m_3}}}{3},\,\frac{{{n_1} + {n_2} + {n_3}}}{3}$$
C.
$$\frac{1}{{\sqrt 3 }}\left( {{l_1} + {l_2} + {l_3}} \right),\,\frac{1}{{\sqrt 3 }}\left( {{m_1} + {m_2} + {m_3}} \right),\,\frac{1}{{\sqrt 3 }}\left( {{n_1} + {n_2} + {n_3}} \right)$$
D.
$$\frac{{{l_1}{l_2}{l_3}}}{{\sqrt 3 }},\,\frac{{{m_1}{m_2}{m_3}}}{{\sqrt 3 }},\,\frac{{{n_1}{n_2}{n_3}}}{{\sqrt 3 }}$$
Answer :
$$\frac{1}{{\sqrt 3 }}\left( {{l_1} + {l_2} + {l_3}} \right),\,\frac{1}{{\sqrt 3 }}\left( {{m_1} + {m_2} + {m_3}} \right),\,\frac{1}{{\sqrt 3 }}\left( {{n_1} + {n_2} + {n_3}} \right)$$
Solution :
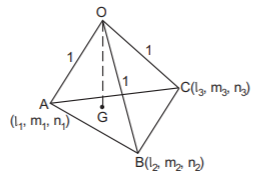
Let $$OA = OB = OC = 1$$ and their direction cosines are $${l_1},\,{m_1},\,{n_1};\,{l_2},\,{m_2},\,{n_2}$$ and $${l_3},\,{m_3},\,{n_3}$$ respectively.
Then $$A = \left( {{l_1},\,{m_1},\,{n_1}} \right),\,B = \left( {{l_2},\,{m_2},\,{n_2}} \right),\,C = \left( {{l_3},\,{m_3},\,{n_3}} \right)$$
and $$OA \bot OB,\,OB \bot OC,\,OC \bot OA.$$
Clearly, $$ABC$$ is equilateral, and $$OG$$ is equally inclined with $$OA,\,OB,\,OC$$ where $$G$$ is the centroid (also circumcentre) of the $$\Delta ABC.$$
$$G = \left( {\frac{{{l_1} + {l_2} + {l_3}}}{3},\,\frac{{{m_1} + {m_2} + {m_3}}}{3},\,\frac{{{n_1} + {n_2} + {n_3}}}{3}} \right)$$
$$\therefore $$ direction ratios of $$OG = {l_1} + {l_2} + {l_3},\,{m_1} + {m_2} + {m_3},\,{n_1} + {n_2} + {n_3}$$
$$\eqalign{ & {\text{Also,}}\,{\left( {{l_1} + {l_2} + {l_3}} \right)^2} + {\left( {{m_1} + {m_2} + {m_3}} \right)^2} + {\left( {{n_1} + {n_2} + {n_3}} \right)^2} \cr & = \sum {l_1^2} + \sum {l_2^2} + \sum {l_3^2 + 2\sum {{l_1}{l_2}} + 2\sum {{l_2}{l_3} + 2\sum {{l_3}{l_1}} } } \cr & = 1 + 1 + 1 + 0 \cr & = 3, \cr} $$
from the conditions of the problem.
$$\therefore $$ direction cosines of $$OG$$ are $$\frac{{{l_1} + {l_2} + {l_3}}}{{\sqrt 3 }},\,\frac{{{m_1} + {m_2} + {m_3}}}{{\sqrt 3 }},\,\frac{{{n_1} + {n_2} + {n_3}}}{{\sqrt 3 }}.$$

Let $$OA = OB = OC = 1$$ and their direction cosines are $${l_1},\,{m_1},\,{n_1};\,{l_2},\,{m_2},\,{n_2}$$ and $${l_3},\,{m_3},\,{n_3}$$ respectively.
Then $$A = \left( {{l_1},\,{m_1},\,{n_1}} \right),\,B = \left( {{l_2},\,{m_2},\,{n_2}} \right),\,C = \left( {{l_3},\,{m_3},\,{n_3}} \right)$$
and $$OA \bot OB,\,OB \bot OC,\,OC \bot OA.$$
Clearly, $$ABC$$ is equilateral, and $$OG$$ is equally inclined with $$OA,\,OB,\,OC$$ where $$G$$ is the centroid (also circumcentre) of the $$\Delta ABC.$$
$$G = \left( {\frac{{{l_1} + {l_2} + {l_3}}}{3},\,\frac{{{m_1} + {m_2} + {m_3}}}{3},\,\frac{{{n_1} + {n_2} + {n_3}}}{3}} \right)$$
$$\therefore $$ direction ratios of $$OG = {l_1} + {l_2} + {l_3},\,{m_1} + {m_2} + {m_3},\,{n_1} + {n_2} + {n_3}$$
$$\eqalign{ & {\text{Also,}}\,{\left( {{l_1} + {l_2} + {l_3}} \right)^2} + {\left( {{m_1} + {m_2} + {m_3}} \right)^2} + {\left( {{n_1} + {n_2} + {n_3}} \right)^2} \cr & = \sum {l_1^2} + \sum {l_2^2} + \sum {l_3^2 + 2\sum {{l_1}{l_2}} + 2\sum {{l_2}{l_3} + 2\sum {{l_3}{l_1}} } } \cr & = 1 + 1 + 1 + 0 \cr & = 3, \cr} $$
from the conditions of the problem.
$$\therefore $$ direction cosines of $$OG$$ are $$\frac{{{l_1} + {l_2} + {l_3}}}{{\sqrt 3 }},\,\frac{{{m_1} + {m_2} + {m_3}}}{{\sqrt 3 }},\,\frac{{{n_1} + {n_2} + {n_3}}}{{\sqrt 3 }}.$$