Question
Locus of mid point of the portion between the axes of $$x\,\cos \,\alpha + y\,\sin \,\alpha = p$$ where $$p$$ is constant is-
A.
$${x^2} + {y^2} = \frac{4}{{{p^2}}}$$
B.
$${x^2} + {y^2} = 4{p^2}$$
C.
$$\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{2}{{{p^2}}}$$
D.
$$\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{4}{{{p^2}}}$$
Answer :
$$\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{4}{{{p^2}}}$$
Solution :
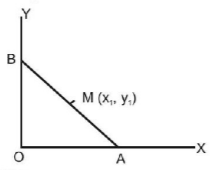
Equation of $$AB$$ is $$x\,\cos \,\alpha + y\,\sin \,\alpha = p;$$
$$\eqalign{ & \Rightarrow \frac{{x\,\cos \,\alpha }}{p} + \frac{{y{\mkern 1mu} \sin \,\alpha }}{p} = 1; \cr & \Rightarrow \frac{x}{{\frac{p}{{\cos \,\alpha }}}} + \frac{y}{{\frac{p}{{\sin \,\alpha }}}} = 1 \cr} $$
So co-ordinates of $$A$$ and $$B$$ are $$\left( {\frac{p}{{\cos \,\alpha }},\,0} \right){\text{ and }}\left( {0,\,\frac{p}{{\sin \,\alpha }}} \right);$$
So coordinates of midpoint of $$AB$$ are
$$\eqalign{ & \left( {\frac{p}{{2\,\cos \,\alpha }},\,\,\frac{p}{{2\,\sin \,\alpha }}} \right) = \left( {{x_1},\,{y_1}} \right)\left( {{\text{let}}} \right); \cr & {x_1} = \frac{p}{{2\,\cos \,\alpha }}\,\,\& \,\,{y_1} = \frac{p}{{2\,\sin \,\alpha }}; \cr & \Rightarrow \cos \,\alpha = \frac{p}{{2{x_1}}}\,\,\,{\text{and}}\,\,{\text{sin}}\,\alpha = \frac{p}{{2{y_1}}};\, \cr & {\cos ^2}\alpha + {\sin ^2}\alpha = 1 \cr & \Rightarrow \frac{{{p^2}}}{4}\left( {\frac{1}{{{x_1}^2}} + \frac{1}{{{y_1}^2}}} \right) = 1 \cr & {\text{Locus of}}\left( {{x_1},\,{y_1}} \right)\,{\text{is }}\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{4}{{{p^2}}}{\text{ }} \cr} $$

Equation of $$AB$$ is $$x\,\cos \,\alpha + y\,\sin \,\alpha = p;$$
$$\eqalign{ & \Rightarrow \frac{{x\,\cos \,\alpha }}{p} + \frac{{y{\mkern 1mu} \sin \,\alpha }}{p} = 1; \cr & \Rightarrow \frac{x}{{\frac{p}{{\cos \,\alpha }}}} + \frac{y}{{\frac{p}{{\sin \,\alpha }}}} = 1 \cr} $$
So co-ordinates of $$A$$ and $$B$$ are $$\left( {\frac{p}{{\cos \,\alpha }},\,0} \right){\text{ and }}\left( {0,\,\frac{p}{{\sin \,\alpha }}} \right);$$
So coordinates of midpoint of $$AB$$ are
$$\eqalign{ & \left( {\frac{p}{{2\,\cos \,\alpha }},\,\,\frac{p}{{2\,\sin \,\alpha }}} \right) = \left( {{x_1},\,{y_1}} \right)\left( {{\text{let}}} \right); \cr & {x_1} = \frac{p}{{2\,\cos \,\alpha }}\,\,\& \,\,{y_1} = \frac{p}{{2\,\sin \,\alpha }}; \cr & \Rightarrow \cos \,\alpha = \frac{p}{{2{x_1}}}\,\,\,{\text{and}}\,\,{\text{sin}}\,\alpha = \frac{p}{{2{y_1}}};\, \cr & {\cos ^2}\alpha + {\sin ^2}\alpha = 1 \cr & \Rightarrow \frac{{{p^2}}}{4}\left( {\frac{1}{{{x_1}^2}} + \frac{1}{{{y_1}^2}}} \right) = 1 \cr & {\text{Locus of}}\left( {{x_1},\,{y_1}} \right)\,{\text{is }}\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{4}{{{p^2}}}{\text{ }} \cr} $$