Question
Let $${x^2} + 3{y^2} = 3$$ be the equation of an ellipse in the $$x$$-$$y$$ plane. $$A$$ and $$B$$ are two points whose position vectors are $$ - \sqrt 3 \hat i$$ and $$ - \sqrt 3 \hat i + 2\hat k.$$ Then the position vector of a point $$P$$ on the ellipse such that $$\angle APB = \frac{\pi }{4}$$ is :
A.
$$ \pm \hat j$$
B.
$$ \pm \left( {\hat i + \hat j} \right)$$
C.
$$ \pm \hat i$$
D.
none of these
Answer :
$$ \pm \hat j$$
Solution :
Point $$P$$ lies on $${x^2} + 3{y^2} = 3......\left( {\text{i}} \right)$$
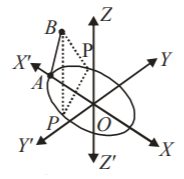
Now from the diagram, according to the given conditions,
$$\eqalign{ & AP = AB{\text{ or }}{\left( {x + \sqrt 3 } \right)^2} + {\left( {y - 0} \right)^2} = 4 \cr & {\text{or }}{\left( {x + \sqrt 3 } \right)^2} + {y^2} = 4......\left( {{\text{ii}}} \right) \cr} $$
Solving $$\left( {\text{i}} \right)$$ and $$\left( {\text{ii}} \right),$$ we get $$x = 0$$ and $$y = \pm 1$$
Hence, point $$P$$ has position vector $$ \pm \hat j.$$
Point $$P$$ lies on $${x^2} + 3{y^2} = 3......\left( {\text{i}} \right)$$

Now from the diagram, according to the given conditions,
$$\eqalign{ & AP = AB{\text{ or }}{\left( {x + \sqrt 3 } \right)^2} + {\left( {y - 0} \right)^2} = 4 \cr & {\text{or }}{\left( {x + \sqrt 3 } \right)^2} + {y^2} = 4......\left( {{\text{ii}}} \right) \cr} $$
Solving $$\left( {\text{i}} \right)$$ and $$\left( {\text{ii}} \right),$$ we get $$x = 0$$ and $$y = \pm 1$$
Hence, point $$P$$ has position vector $$ \pm \hat j.$$