Question
Let $$S$$ be the set of all complex numbers $$z$$ satisfying $$\left| {z - 2 + i} \right|\, \geqslant \sqrt 5 .$$ If the complex number $${z_0}$$ is such that $$\frac{1}{{\left| {{z_0} - 1} \right|}}$$ is the maximum of the set $$\left\{ {\frac{1}{{\left| {z - 1} \right|}}:z \in S} \right\},$$ then the principal argument of $$\frac{{4 - {z_0} - {{\overline z }_0}}}{{{z_0} - {{\overline z }_0} + 2i}}$$ is
A.
$$\frac{\pi }{4}$$
B.
$$\frac{{3\pi }}{4}$$
C.
$$\frac{\pi }{2}$$
D.
$$ - \frac{\pi }{2}$$
Answer :
$$ - \frac{\pi }{2}$$
Solution :
$$S:\left| {z - 2 + i} \right|\, \geqslant \sqrt 5 $$ represents boundary and outer region of circle with center $$\left( {2, - 1} \right)$$ and radius $$\sqrt 5 $$
$${{z_0} \in S},$$ such that $$\frac{1}{{\left| {{z_0} - 1} \right|}}$$ is the maximum.
∴ $${\left| {{z_0} - 1} \right|}$$ is minimum
$${{z_0} \in S}$$ with $${\left| {{z_0} - 1} \right|}$$ as minimum will be a point on boundary of circle of region $$S$$ which lies on radius of this circle, which passes through (1, 0).
$$\therefore \,\,{z_0},1,2 - i$$ are collinear, or $$\left( {{x_0},{y_0}} \right),\left( {1,0} \right),\left( {2, - 1} \right)$$ are collinear.
∴ Using slopes of paralled lines,
$$\eqalign{ & \frac{{{y_0}}}{{{x_0} - 1}} = \frac{{ - 1}}{{2 - 1}} \cr & \Rightarrow \,\,{y_0} = 1 - {x_0} \cr} $$
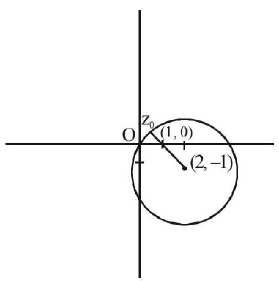
$$\eqalign{ & {\text{Now, }}\frac{{4 - {z_0} - {{\overline z }_0}}}{{{z_0} - {{\overline z }_0} + 2i}} \cr & = \frac{{4 - \left( {{z_0} + {{\overline z }_0}} \right)}}{{\left( {{z_0} - {{\overline z }_0}} \right) + 2i}} \cr & = \frac{{4 - 2{x_0}}}{{2i{y_0} + 2i}} \cr & = \frac{{4 - 2{x_0}}}{{2i - 2{x_0}i + 2i}} \cr & = \frac{{2\left( {2 - {x_0}} \right)}}{{2\left( {2 - {x_0}} \right)}i} \cr & = \frac{1}{i} = - i \cr & \therefore \,\,Arg\left( {\frac{{4 - {z_0} - {{\overline z }_0}}}{{{z_0} - {{\overline z }_0} - 2i}}} \right) \cr & = Arg\left( { - i} \right) \cr & = \frac{{ - \pi }}{2} \cr} $$
$$S:\left| {z - 2 + i} \right|\, \geqslant \sqrt 5 $$ represents boundary and outer region of circle with center $$\left( {2, - 1} \right)$$ and radius $$\sqrt 5 $$
$${{z_0} \in S},$$ such that $$\frac{1}{{\left| {{z_0} - 1} \right|}}$$ is the maximum.
∴ $${\left| {{z_0} - 1} \right|}$$ is minimum
$${{z_0} \in S}$$ with $${\left| {{z_0} - 1} \right|}$$ as minimum will be a point on boundary of circle of region $$S$$ which lies on radius of this circle, which passes through (1, 0).
$$\therefore \,\,{z_0},1,2 - i$$ are collinear, or $$\left( {{x_0},{y_0}} \right),\left( {1,0} \right),\left( {2, - 1} \right)$$ are collinear.
∴ Using slopes of paralled lines,
$$\eqalign{ & \frac{{{y_0}}}{{{x_0} - 1}} = \frac{{ - 1}}{{2 - 1}} \cr & \Rightarrow \,\,{y_0} = 1 - {x_0} \cr} $$
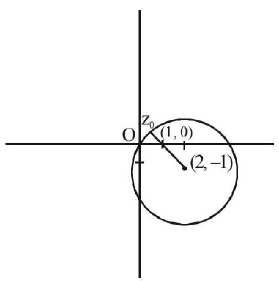
$$\eqalign{ & {\text{Now, }}\frac{{4 - {z_0} - {{\overline z }_0}}}{{{z_0} - {{\overline z }_0} + 2i}} \cr & = \frac{{4 - \left( {{z_0} + {{\overline z }_0}} \right)}}{{\left( {{z_0} - {{\overline z }_0}} \right) + 2i}} \cr & = \frac{{4 - 2{x_0}}}{{2i{y_0} + 2i}} \cr & = \frac{{4 - 2{x_0}}}{{2i - 2{x_0}i + 2i}} \cr & = \frac{{2\left( {2 - {x_0}} \right)}}{{2\left( {2 - {x_0}} \right)}i} \cr & = \frac{1}{i} = - i \cr & \therefore \,\,Arg\left( {\frac{{4 - {z_0} - {{\overline z }_0}}}{{{z_0} - {{\overline z }_0} - 2i}}} \right) \cr & = Arg\left( { - i} \right) \cr & = \frac{{ - \pi }}{2} \cr} $$