Question
Let $$f\left( x \right) = \left| {x - 2} \right| + \left| {x - 3} \right| + \left| {x - 4} \right|$$ and $$g\left( x \right) = f\left( {x + 1} \right).$$ Then :
A.
$$g\left( x \right)$$ is an even function
B.
$$g\left( x \right)$$ is an odd function
C.
$$g\left( x \right)$$ is neither even nor odd
D.
$$g\left( x \right)$$ is periodic
Answer :
$$g\left( x \right)$$ is neither even nor odd
Solution :
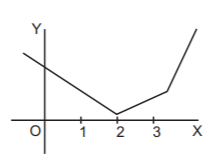
$$\eqalign{ & g\left( x \right) = f\left( {x + 1} \right) = \left| {x - 1} \right| + \left| {x - 2} \right| + \left| {x - 3} \right| \cr & {\text{If }}x < 1,\,\,\,g\left( x \right) = - x + 1 - x + 2 - x + 3 = - 3x + 6 \cr & {\text{If 1}} \leqslant x < 2,\,\,\,g\left( x \right) = x - 1 - x + 2 - x + 3 = - x + 4 \cr & {\text{If 2}} \leqslant x < 3,\,\,\,g\left( x \right) = x - 1 + x - 2 - x + 3 = x \cr & {\text{If }}x \geqslant 3,\,\,\,g\left( x \right) = x - 1 + x - 2 + x - 3 = 3x - 6 \cr} $$

$$\eqalign{ & g\left( x \right) = f\left( {x + 1} \right) = \left| {x - 1} \right| + \left| {x - 2} \right| + \left| {x - 3} \right| \cr & {\text{If }}x < 1,\,\,\,g\left( x \right) = - x + 1 - x + 2 - x + 3 = - 3x + 6 \cr & {\text{If 1}} \leqslant x < 2,\,\,\,g\left( x \right) = x - 1 - x + 2 - x + 3 = - x + 4 \cr & {\text{If 2}} \leqslant x < 3,\,\,\,g\left( x \right) = x - 1 + x - 2 - x + 3 = x \cr & {\text{If }}x \geqslant 3,\,\,\,g\left( x \right) = x - 1 + x - 2 + x - 3 = 3x - 6 \cr} $$