Question
Let $$f:R \to R$$ be a function defined by $$f\left( x \right) = \min \left\{ {x + 1,\,\left| x \right| + 1} \right\},$$
Let $$f:R \to R$$ be a function defined by $$f\left( x \right) = \min \left\{ {x + 1,\,\left| x \right| + 1} \right\},$$
Then which of the following is true?
A.
$$f\left( x \right)$$ is differentiable everywhere
B.
$$f\left( x \right)$$ is not differentiable at $$x =0$$
C.
$$f\left( x \right) \geqslant 1{\text{ for all }}x \in R$$
D.
$$f\left( x \right)$$ is not differentiable at $$x =1$$
Answer :
$$f\left( x \right)$$ is differentiable everywhere
Solution :
$$\eqalign{ & f\left( x \right) = \min \left\{ {x + 1,\,\left| x \right| + 1} \right\} \cr & \Rightarrow f\left( x \right) = x + 1\,\forall \,x \in R \cr} $$
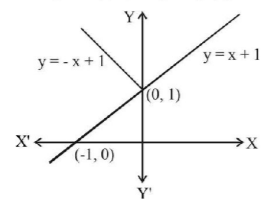
Hence, $$f\left( x \right)$$ is differentiable everywhere for all $$x \in R.$$
$$\eqalign{ & f\left( x \right) = \min \left\{ {x + 1,\,\left| x \right| + 1} \right\} \cr & \Rightarrow f\left( x \right) = x + 1\,\forall \,x \in R \cr} $$

Hence, $$f\left( x \right)$$ is differentiable everywhere for all $$x \in R.$$