Question
Let $$f:\left[ {0,\,1} \right] \to \left[ {0,\,1} \right]$$ be a continuous function. Then :
A.
$$f\left( x \right) = x$$ for at least one $$0 \leqslant x \leqslant 1$$
B.
$$f\left( x \right)$$ will be differentiable in $$\left[ {0,\,1} \right]$$
C.
$$f\left( x \right) + x = 0$$ for at least one $$x$$ such that $$0 \leqslant x \leqslant 1$$
D.
none of these
Answer :
$$f\left( x \right) = x$$ for at least one $$0 \leqslant x \leqslant 1$$
Solution :
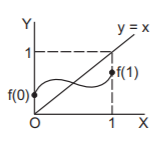
Clearly, $$0 \leqslant f\left( 0 \right) \leqslant 1$$ and $$0 \leqslant f\left( 1 \right) \leqslant 1.$$ As $$f\left( x \right)$$ is continuous, $$f\left( x \right)$$ attains all values between $$f\left( 0 \right)$$ to $$f\left( 1 \right),$$ and the graph will have no breaks. So, the graph will cut the line $$y=x$$ at one point $$x$$ at least where $$0 \leqslant x \leqslant 1.$$ So, $$f\left( x \right) = x$$ at that point.
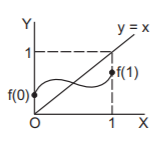
Clearly, $$0 \leqslant f\left( 0 \right) \leqslant 1$$ and $$0 \leqslant f\left( 1 \right) \leqslant 1.$$ As $$f\left( x \right)$$ is continuous, $$f\left( x \right)$$ attains all values between $$f\left( 0 \right)$$ to $$f\left( 1 \right),$$ and the graph will have no breaks. So, the graph will cut the line $$y=x$$ at one point $$x$$ at least where $$0 \leqslant x \leqslant 1.$$ So, $$f\left( x \right) = x$$ at that point.