Question
Let $$C$$ be the circle with centre $$\left( {0,\,0} \right)$$ and radius $$3$$ units. The equation of the locus of the mid points of the chords of the circle $$C$$ that subtend an angle of $$\frac{{2\pi }}{3}$$ at its center is-
A.
$${x^2} + {y^2} = \frac{3}{2}$$
B.
$${x^2} + {y^2} = 1$$
C.
$${x^2} + {y^2} = \frac{{27}}{4}$$
D.
$${x^2} + {y^2} = \frac{9}{4}$$
Answer :
$${x^2} + {y^2} = \frac{9}{4}$$
Solution :
Let $$M\left( {h,\,k} \right)$$ be the mid point of chord $$AB$$ where
$$\angle AOB = \frac{{2\pi }}{3}$$
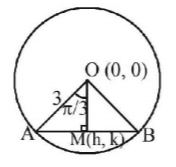
$$\eqalign{ & \therefore \angle AOM = \frac{\pi }{3},{\text{ Also }}OM = 3\,\cos \frac{\pi }{3} = \frac{3}{2} \cr & \Rightarrow \sqrt {{h^2} + {k^2}} = \frac{3}{2} \Rightarrow {h^2} + {k^2} = \frac{9}{4} \cr} $$
$$\therefore $$ Locus of $$\left( {h,\,k} \right)$$ is $${x^2} + {y^2} = \frac{9}{4}$$
Let $$M\left( {h,\,k} \right)$$ be the mid point of chord $$AB$$ where
$$\angle AOB = \frac{{2\pi }}{3}$$

$$\eqalign{ & \therefore \angle AOM = \frac{\pi }{3},{\text{ Also }}OM = 3\,\cos \frac{\pi }{3} = \frac{3}{2} \cr & \Rightarrow \sqrt {{h^2} + {k^2}} = \frac{3}{2} \Rightarrow {h^2} + {k^2} = \frac{9}{4} \cr} $$
$$\therefore $$ Locus of $$\left( {h,\,k} \right)$$ is $${x^2} + {y^2} = \frac{9}{4}$$