Question
Let $$ABCD$$ be a quadrilateral with area 18, with side $$AB$$ parallel to the side $$CD$$ and $$2AB = CD.$$ Let $$AD$$ be perpendicular to $$AB$$ and $$CD.$$ If a circle is drawn inside the quadrilateral $$ABCD$$ touching all the sides, then its radius is
A.
3
B.
2
C.
$$\frac{3}{2}$$
D.
1
Answer :
2
Solution :
$${\text{Given }}AB\parallel CD,$$ $$CD = 2AB$$
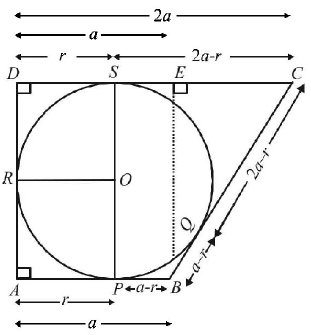
Let $$AB = a$$ then $$CD = 2a$$ Let radius of circle be $$r.$$ Let circle touches $$AB$$ at $$P, BC$$ at $$Q, AD$$ at $$R$$ and $$CD$$ at $$S.$$
Then $$AR = AP = r, BP = BQ = a - r$$
$$DR = DS = r$$ and $$CQ = CS = 2a - r$$ In $$\Delta BEC$$
$$\eqalign{ & B{C^2} = B{E^2} + E{C^2} \cr & \Rightarrow \,\,{\left( {a - r + 2a - r} \right)^2} = {\left( {2r} \right)^2} + {\left( a \right)^2} \cr & \Rightarrow \,\,9{a^2} + 4{r^2} - 12ar = 4{r^2} + {a^2} \cr & \Rightarrow \,\,a = \frac{3}{2}r\,\,\,\,\,\,\,.....\left( 1 \right) \cr} $$
Also $$Ar$$ (quad. $$ABCD$$ ) $$=$$ 18
$$\eqalign{ & \Rightarrow \,\,a \times 2r + \frac{1}{2} \times a \times 2r = 18 \cr & \Rightarrow \,\,ar = 6 \cr & \Rightarrow \,\,\frac{{3{r^2}}}{2} = 6\,\left( {{\text{using equation }}\left( 1 \right)} \right) \cr & \Rightarrow \,\,{r^2} = 4 \cr & \Rightarrow \,\,r = 2 \cr} $$
$${\text{Given }}AB\parallel CD,$$ $$CD = 2AB$$
Let $$AB = a$$ then $$CD = 2a$$ Let radius of circle be $$r.$$ Let circle touches $$AB$$ at $$P, BC$$ at $$Q, AD$$ at $$R$$ and $$CD$$ at $$S.$$
Then $$AR = AP = r, BP = BQ = a - r$$
$$DR = DS = r$$ and $$CQ = CS = 2a - r$$ In $$\Delta BEC$$
$$\eqalign{ & B{C^2} = B{E^2} + E{C^2} \cr & \Rightarrow \,\,{\left( {a - r + 2a - r} \right)^2} = {\left( {2r} \right)^2} + {\left( a \right)^2} \cr & \Rightarrow \,\,9{a^2} + 4{r^2} - 12ar = 4{r^2} + {a^2} \cr & \Rightarrow \,\,a = \frac{3}{2}r\,\,\,\,\,\,\,.....\left( 1 \right) \cr} $$
Also $$Ar$$ (quad. $$ABCD$$ ) $$=$$ 18

$$\eqalign{ & \Rightarrow \,\,a \times 2r + \frac{1}{2} \times a \times 2r = 18 \cr & \Rightarrow \,\,ar = 6 \cr & \Rightarrow \,\,\frac{{3{r^2}}}{2} = 6\,\left( {{\text{using equation }}\left( 1 \right)} \right) \cr & \Rightarrow \,\,{r^2} = 4 \cr & \Rightarrow \,\,r = 2 \cr} $$