Question
Let $$\overrightarrow {AB} = 3\overrightarrow i + \overrightarrow j - \overrightarrow k $$ and $$\overrightarrow {AC} = \overrightarrow i - \overrightarrow j + 3\overrightarrow k .$$ If the point $$P$$ on the line segment $$BC$$ is equidistant from $$AB$$ and $$AC$$ then $$\overrightarrow {AP} $$ is :
A.
$$2\overrightarrow i - \overrightarrow k $$
B.
$$\overrightarrow i - 2\overrightarrow k $$
C.
$$2\overrightarrow i + \overrightarrow k $$
D.
none of these
Answer :
$$2\overrightarrow i + \overrightarrow k $$
Solution :
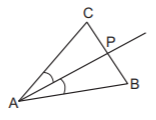
A point equidistant from $$AB$$ and $$AC$$ is on the bisectors of the angle $$BAC.$$
A vector along the internal bisector of the angle $$BAC$$
$$\eqalign{ & = \frac{{\overrightarrow {AB} }}{{\left| {\overrightarrow {AB} } \right|}} + \frac{{\overrightarrow {AC} }}{{\left| {\overrightarrow {AC} } \right|}} \cr & = \frac{{3\overrightarrow i + \overrightarrow j - \overrightarrow k }}{{\sqrt {{3^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} + \frac{{\overrightarrow i - \overrightarrow j + 3\overrightarrow k }}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {3^2}} }} \cr & = \frac{1}{{\sqrt {11} }}\left( {4\overrightarrow i + 2\overrightarrow k } \right) \cr & \therefore \,\overrightarrow {AP} = t\left( {2\overrightarrow i + \overrightarrow k } \right) \cr & \therefore \,\overrightarrow {BP} = \overrightarrow {AP} - \overrightarrow {AB} = t\left( {2\overrightarrow i + \overrightarrow k } \right) - \left( {3\overrightarrow i + \overrightarrow j - \overrightarrow k } \right) \cr & \therefore \,\overrightarrow {BP} = \left( {2t - 3} \right)\overrightarrow i - \overrightarrow j + \left( {t + 1} \right)\overrightarrow k \cr & {\text{Also,}}\,\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} = \left( {\overrightarrow i - \overrightarrow j + 3\overrightarrow k } \right) - \left( {3\overrightarrow i + \overrightarrow j - \overrightarrow k } \right) = - 2\overrightarrow i - 2\overrightarrow j + 4\overrightarrow k \cr & {\text{But }}\overrightarrow {BP} = s\overrightarrow {BC} \cr & \therefore \,\left( {2t - 3} \right)\overrightarrow i - \overrightarrow j + \left( {t + 1} \right)\overrightarrow k = s\left( { - 2\overrightarrow i - 2\overrightarrow j + 4\overrightarrow k } \right) \cr & {\text{or }}2t - 3 = - 2s,\,\,\, - 1 = - 2s,\,\,\,t + 1 = 4s \cr & \therefore \,s = \frac{1}{2}{\text{ and }}t = 1 \cr & \therefore \,\overrightarrow {AP} = 2\overrightarrow i + \overrightarrow k . \cr} $$

A point equidistant from $$AB$$ and $$AC$$ is on the bisectors of the angle $$BAC.$$
A vector along the internal bisector of the angle $$BAC$$
$$\eqalign{ & = \frac{{\overrightarrow {AB} }}{{\left| {\overrightarrow {AB} } \right|}} + \frac{{\overrightarrow {AC} }}{{\left| {\overrightarrow {AC} } \right|}} \cr & = \frac{{3\overrightarrow i + \overrightarrow j - \overrightarrow k }}{{\sqrt {{3^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} + \frac{{\overrightarrow i - \overrightarrow j + 3\overrightarrow k }}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {3^2}} }} \cr & = \frac{1}{{\sqrt {11} }}\left( {4\overrightarrow i + 2\overrightarrow k } \right) \cr & \therefore \,\overrightarrow {AP} = t\left( {2\overrightarrow i + \overrightarrow k } \right) \cr & \therefore \,\overrightarrow {BP} = \overrightarrow {AP} - \overrightarrow {AB} = t\left( {2\overrightarrow i + \overrightarrow k } \right) - \left( {3\overrightarrow i + \overrightarrow j - \overrightarrow k } \right) \cr & \therefore \,\overrightarrow {BP} = \left( {2t - 3} \right)\overrightarrow i - \overrightarrow j + \left( {t + 1} \right)\overrightarrow k \cr & {\text{Also,}}\,\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} = \left( {\overrightarrow i - \overrightarrow j + 3\overrightarrow k } \right) - \left( {3\overrightarrow i + \overrightarrow j - \overrightarrow k } \right) = - 2\overrightarrow i - 2\overrightarrow j + 4\overrightarrow k \cr & {\text{But }}\overrightarrow {BP} = s\overrightarrow {BC} \cr & \therefore \,\left( {2t - 3} \right)\overrightarrow i - \overrightarrow j + \left( {t + 1} \right)\overrightarrow k = s\left( { - 2\overrightarrow i - 2\overrightarrow j + 4\overrightarrow k } \right) \cr & {\text{or }}2t - 3 = - 2s,\,\,\, - 1 = - 2s,\,\,\,t + 1 = 4s \cr & \therefore \,s = \frac{1}{2}{\text{ and }}t = 1 \cr & \therefore \,\overrightarrow {AP} = 2\overrightarrow i + \overrightarrow k . \cr} $$