Question
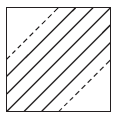
In the given square, a diagonal is drawn, and parallel line segments joining points on the adjacent sides are drawn on both sides of the diagonal. The length of the diagonal is $$n\sqrt 2 \,cm.$$ If the distance between consecutive line segments be $$\frac{1}{{\sqrt 2 }}\,cm$$ then the sum of the lengths of all possible line segments and the diagonal is
In the given square, a diagonal is drawn, and parallel line segments joining points on the adjacent sides are drawn on both sides of the diagonal. The length of the diagonal is $$n\sqrt 2 \,cm.$$ If the distance between consecutive line segments be $$\frac{1}{{\sqrt 2 }}\,cm$$ then the sum of the lengths of all possible line segments and the diagonal is
A.
$$n\left( {n + 1} \right)\sqrt 2 \,cm$$
B.
$${n^2}\,cm$$
C.
$$n\left( {n + 2} \right)\,cm$$
D.
$${n^2}\sqrt 2 \,cm$$
Answer :
$${n^2}\sqrt 2 \,cm$$
Solution :
Lengths of line segments on one side of the diagonal are
$$\sqrt 2 ,2\sqrt 2 ,3\sqrt 2 ,.....,\left( {n - 1} \right)\sqrt 2 .$$
So, the required sum $$ = 2\left\{ {\sqrt 2 + 2\sqrt 2 + 3\sqrt 2 + ..... + \left( {n - 1} \right)\sqrt 2 } \right\} + n\sqrt 2 $$
$$ = 2\sqrt 2 \left\{ {1 + 2 + 3 + ..... + \left( {n - 1} \right)} \right\} + n\sqrt 2 .$$
Lengths of line segments on one side of the diagonal are
$$\sqrt 2 ,2\sqrt 2 ,3\sqrt 2 ,.....,\left( {n - 1} \right)\sqrt 2 .$$
So, the required sum $$ = 2\left\{ {\sqrt 2 + 2\sqrt 2 + 3\sqrt 2 + ..... + \left( {n - 1} \right)\sqrt 2 } \right\} + n\sqrt 2 $$
$$ = 2\sqrt 2 \left\{ {1 + 2 + 3 + ..... + \left( {n - 1} \right)} \right\} + n\sqrt 2 .$$