Question
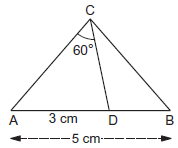
In the figure, $$ABC$$ is a triangle in which $$C = {90^ \circ }$$ and $$AB = 5\,cm.$$ $$D$$ is a point on $$AB$$ such that $$AD = 3\,cm$$ and $$\angle ACD = {60^ \circ }.$$ Then the length of $$AC$$ is
In the figure, $$ABC$$ is a triangle in which $$C = {90^ \circ }$$ and $$AB = 5\,cm.$$ $$D$$ is a point on $$AB$$ such that $$AD = 3\,cm$$ and $$\angle ACD = {60^ \circ }.$$ Then the length of $$AC$$ is
A.
$$5\sqrt {\frac{3}{7}} \,cm$$
B.
$$\sqrt {\frac{7}{3}} \,cm$$
C.
$$\frac{3}{{\sqrt 7 }}\,cm$$
D.
None of these
Answer :
$$5\sqrt {\frac{3}{7}} \,cm$$
Solution :
Using $$\left( {m + n} \right)\cot \theta = n\cot \beta - m\cot \alpha ,$$ we get,
$$\eqalign{ & \left( {3 + 2} \right)\cot \angle CDA = 2\cot {30^ \circ } - 3\cot {60^ \circ } \cr & \Rightarrow \,\,\cot \angle CDA = \frac{{\sqrt 3 }}{5}. \cr} $$
Now use sine rule in $$\vartriangle CDA.$$
Using $$\left( {m + n} \right)\cot \theta = n\cot \beta - m\cot \alpha ,$$ we get,
$$\eqalign{ & \left( {3 + 2} \right)\cot \angle CDA = 2\cot {30^ \circ } - 3\cot {60^ \circ } \cr & \Rightarrow \,\,\cot \angle CDA = \frac{{\sqrt 3 }}{5}. \cr} $$
Now use sine rule in $$\vartriangle CDA.$$