Question
In a $$\vartriangle ABC,$$ $$I$$ is the incentre. The ratio $$IA : IB : IC$$ is equal to
A.
$${\text{cosec}}\frac{A}{2}:{\text{cosec}}\frac{B}{2}:{\text{cosec}}\frac{C}{2}$$
B.
$$\sin \frac{A}{2}:\sin \frac{B}{2}:\sin \frac{C}{2}$$
C.
$$\sec \frac{A}{2}:\sec \frac{B}{2}:\sec \frac{C}{2}$$
D.
None of these
Answer :
$${\text{cosec}}\frac{A}{2}:{\text{cosec}}\frac{B}{2}:{\text{cosec}}\frac{C}{2}$$
Solution :
Here, $$BD : DC = c : b.$$
But $$BD + DC = a;$$
$$\therefore \,\,BD = \frac{c}{{b + c}} \cdot a.$$
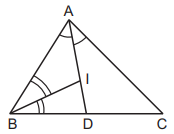
$$\eqalign{ & {\text{In}}\,\,\vartriangle ABD,\frac{{BD}}{{\sin \frac{A}{2}}} = \frac{{AD}}{{\sin B}} \cr & \therefore \,\,AD = \frac{{ca}}{{b + c}} \cdot \frac{{\sin B}}{{\sin \frac{A}{2}}} = \frac{{2\vartriangle }}{{b + c}}{\text{cosec}}\frac{A}{2}. \cr & {\text{Also, }}\frac{{AI}}{{ID}} = \frac{{AB}}{{BD}} = \frac{c}{{\frac{{ca}}{{\left( {b + c} \right)}}}} = \frac{{b + c}}{a} \cr & \Rightarrow \,\,AI = \frac{{b + c}}{{a + b + c}} \cdot AD = \frac{\vartriangle }{s}{\text{cosec}}\frac{A}{2}. \cr} $$
Similarly for $$BI$$ and $$CI.$$
Here, $$BD : DC = c : b.$$
But $$BD + DC = a;$$
$$\therefore \,\,BD = \frac{c}{{b + c}} \cdot a.$$

$$\eqalign{ & {\text{In}}\,\,\vartriangle ABD,\frac{{BD}}{{\sin \frac{A}{2}}} = \frac{{AD}}{{\sin B}} \cr & \therefore \,\,AD = \frac{{ca}}{{b + c}} \cdot \frac{{\sin B}}{{\sin \frac{A}{2}}} = \frac{{2\vartriangle }}{{b + c}}{\text{cosec}}\frac{A}{2}. \cr & {\text{Also, }}\frac{{AI}}{{ID}} = \frac{{AB}}{{BD}} = \frac{c}{{\frac{{ca}}{{\left( {b + c} \right)}}}} = \frac{{b + c}}{a} \cr & \Rightarrow \,\,AI = \frac{{b + c}}{{a + b + c}} \cdot AD = \frac{\vartriangle }{s}{\text{cosec}}\frac{A}{2}. \cr} $$
Similarly for $$BI$$ and $$CI.$$