Question
If $$\left[ y \right] = $$ the greatest integer less than or equal to $$y$$ then $$\int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left[ {2\sin \,x} \right]dx} $$ is :
A.
$$ - \pi $$
B.
0
C.
$$ - \frac{\pi }{2}$$
D.
$$\frac{\pi }{2}$$
Answer :
$$ - \frac{\pi }{2}$$
Solution :
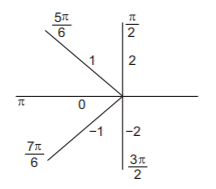
$$\eqalign{ & I = \int_{\frac{\pi }{2}}^{\frac{{5\pi }}{6}} {\left[ {2\sin \,x} \right]dx} + \int_{\frac{{5\pi }}{6}}^\pi {\left[ {2\sin \,x} \right]dx} + \int_\pi ^{\frac{{7\pi }}{6}} {\left[ {2\sin \,x} \right]dx} + \int_{\frac{{7\pi }}{6}}^{\frac{{3\pi }}{2}} {\left[ {2\sin \,x} \right]dx} \cr & \,\,\,\,\, = \int_{\frac{\pi }{2}}^{\frac{{5\pi }}{6}} {1\,dx} + \int_{\frac{{5\pi }}{6}}^\pi {0\,dx} + \int_\pi ^{\frac{{7\pi }}{6}} { - 1\,dx} + \int_{\frac{{7\pi }}{6}}^{\frac{{3\pi }}{2}} { - 2\,dx} \cr & \,\,\,\,\, = \frac{{5\pi }}{6} - \frac{\pi }{2} - \left( {\frac{{7\pi }}{6} - \pi } \right) - 2\left( {\frac{{3\pi }}{2} - \frac{{7\pi }}{6}} \right) \cr & \,\,\,\,\, = - \frac{\pi }{2} \cr} $$

$$\eqalign{ & I = \int_{\frac{\pi }{2}}^{\frac{{5\pi }}{6}} {\left[ {2\sin \,x} \right]dx} + \int_{\frac{{5\pi }}{6}}^\pi {\left[ {2\sin \,x} \right]dx} + \int_\pi ^{\frac{{7\pi }}{6}} {\left[ {2\sin \,x} \right]dx} + \int_{\frac{{7\pi }}{6}}^{\frac{{3\pi }}{2}} {\left[ {2\sin \,x} \right]dx} \cr & \,\,\,\,\, = \int_{\frac{\pi }{2}}^{\frac{{5\pi }}{6}} {1\,dx} + \int_{\frac{{5\pi }}{6}}^\pi {0\,dx} + \int_\pi ^{\frac{{7\pi }}{6}} { - 1\,dx} + \int_{\frac{{7\pi }}{6}}^{\frac{{3\pi }}{2}} { - 2\,dx} \cr & \,\,\,\,\, = \frac{{5\pi }}{6} - \frac{\pi }{2} - \left( {\frac{{7\pi }}{6} - \pi } \right) - 2\left( {\frac{{3\pi }}{2} - \frac{{7\pi }}{6}} \right) \cr & \,\,\,\,\, = - \frac{\pi }{2} \cr} $$