If the vertices of a tetrahedron have the position vectors $$\overrightarrow 0 ,\,\overrightarrow i + \overrightarrow j ,\,2\overrightarrow j - \overrightarrow k $$     and $$\overrightarrow i + \overrightarrow k $$   then the volume of the tetrahedron is :

Solution :

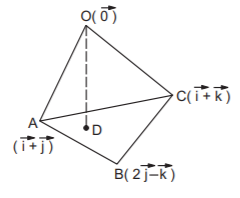
Volume of the tetrahedron $$ = V = \left| {\frac{1}{6}\left[ {\overrightarrow {AB} \,\,\overrightarrow {AC} \,\,\overrightarrow {AO} } \right]} \right|$$
Now,
$$\eqalign{ & \overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = 2\overrightarrow j - \overrightarrow k - \left( {\overrightarrow i + \overrightarrow j } \right) = - \overrightarrow i + \overrightarrow j - \overrightarrow k \cr & \overrightarrow {AC} = \overrightarrow {OC} - \overrightarrow {OA} = \overrightarrow i + \overrightarrow k - \left( {\overrightarrow i + \overrightarrow j } \right) = \overrightarrow k - \overrightarrow j \cr} $$
\[\therefore \,V = \left| {\frac{1}{6}\left[ { - \overrightarrow i + \overrightarrow j - \overrightarrow k \,\,\,\overrightarrow k - \overrightarrow j \,\,\, - \overrightarrow i - \overrightarrow j } \right]} \right| = \left| {\frac{1}{6}\left| \begin{array}{l} - 1\,\,\,\,\,\,\,\,\,\,\,1\,\,\,\,\, - 1\\ \,\,\,\,\,\,0\,\,\,\, - 1\,\,\,\,\,\,\,\,\,\,\,1\\ - 1\,\,\,\, - 1\,\,\,\,\,\,\,\,\,\,\,\,0\, \end{array} \right|} \right| = \frac{1}{6}\]