Question
If the vertex $$ = \left( {2,\,0} \right)$$ and the extremities of the latus rectum are $$\left( {3,\,2} \right)$$ and $$\left( {3,\, - 2} \right)$$ then the equation of the parabola is :
A.
$${y^2} = 2x - 4$$
B.
$${x^2} = 4y - 8$$
C.
$${y^2} = 4x - 8$$
D.
none of these
Answer :
$${y^2} = 4x - 8$$
Solution :
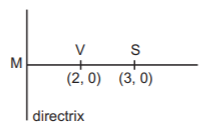
The focus $$ = \left( {\frac{{3 + 3}}{2},\,\frac{{2 - 2}}{2}} \right) = \left( {3,\,0} \right).$$ The vertex $$ = \left( {2,\,0} \right)$$
As $$MV = VS,\,\,M = \left( {1,\,0} \right).$$ Clearly, the directrix is perpendicular to $$VS$$ whose equation is $$y = 0.$$ So, the directrix is $$x = k$$ which passes through $$M\left( {1,\,0} \right).$$ Therefore, we get $$x = 1.$$
$$\therefore $$ the equation of the parabola is $${\left( {x - 3} \right)^2} + {\left( {y - 0} \right)^2} = {\left( {\frac{{x - 1}}{{\sqrt 1 }}} \right)^2}.$$

The focus $$ = \left( {\frac{{3 + 3}}{2},\,\frac{{2 - 2}}{2}} \right) = \left( {3,\,0} \right).$$ The vertex $$ = \left( {2,\,0} \right)$$
As $$MV = VS,\,\,M = \left( {1,\,0} \right).$$ Clearly, the directrix is perpendicular to $$VS$$ whose equation is $$y = 0.$$ So, the directrix is $$x = k$$ which passes through $$M\left( {1,\,0} \right).$$ Therefore, we get $$x = 1.$$
$$\therefore $$ the equation of the parabola is $${\left( {x - 3} \right)^2} + {\left( {y - 0} \right)^2} = {\left( {\frac{{x - 1}}{{\sqrt 1 }}} \right)^2}.$$