Question
If the point $${z_1} = 1 + i$$ where $$i = \sqrt { - 1} $$ is the reflection of a point $${z_2} = x + iy$$ in the line $$i\bar z - i\bar z = 5,$$ then the point $$z_2$$ is
A.
$$1 + 4i$$
B.
$$4 + i$$
C.
$$1 - i$$
D.
$$- 1 - i$$
Answer :
$$1 + 4i$$
Solution :
Let $$z = a + bi$$
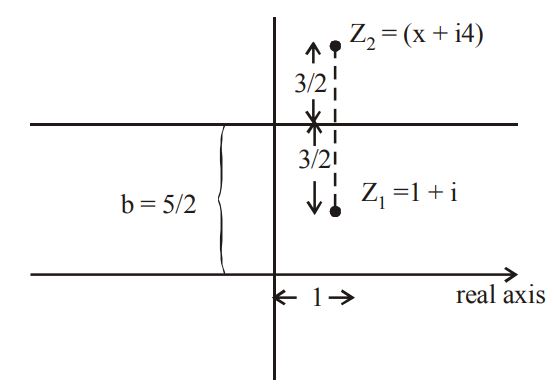
$$\eqalign{ & \Rightarrow \bar z = a - bi \cr & \therefore i\bar z - iz = i\left[ {\left( {a - bi} \right) - \left( {a + bi} \right)} \right] = 5 \cr & \Rightarrow i\left[ { - 2bi} \right] = 5 \cr & \Rightarrow b = \frac{5}{2} \cr} $$
So from figure it is clear that
$$\eqalign{ & x = 1,y = \frac{5}{2} + \frac{3}{2} = 4 \cr & {z_2} = 1 + 4i \cr} $$
Let $$z = a + bi$$

$$\eqalign{ & \Rightarrow \bar z = a - bi \cr & \therefore i\bar z - iz = i\left[ {\left( {a - bi} \right) - \left( {a + bi} \right)} \right] = 5 \cr & \Rightarrow i\left[ { - 2bi} \right] = 5 \cr & \Rightarrow b = \frac{5}{2} \cr} $$
So from figure it is clear that
$$\eqalign{ & x = 1,y = \frac{5}{2} + \frac{3}{2} = 4 \cr & {z_2} = 1 + 4i \cr} $$