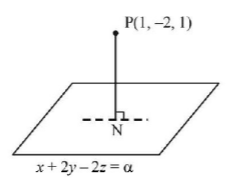
If the distance of the point $$P\left( {1,\, - 2,\,1} \right)$$   from the plane $$x + 2y - 2z = \alpha ,$$    where $$\alpha > 0,$$  is 5, then the foot of the perpendicular from $$P$$ to the plane is :

Solution :
As perpendicular distance of $$x + 2y - 2z = \alpha $$    from the point $$\left( {1,\, - 2,\,1} \right)$$   is 5

$$\eqalign{ & \therefore \left| {\frac{{1 - 4 - 2 - \alpha }}{3}} \right| = 5 \cr & \Rightarrow \frac{{ - 5 - \alpha }}{3} = 5{\text{ or }} - 5 \cr & \Rightarrow \alpha = - 20{\text{ or }}10 \cr & {\text{As }}\alpha > 0\,\,\, \Rightarrow \alpha = 10 \cr} $$
$$\therefore $$ Plane becomes $$x+2y-2z-10=0$$
Equation of PN is $$\frac{{x - 1}}{1} = \frac{{y + 2}}{2} = \frac{{z - 1}}{{ - 2}} = \lambda $$
For some value of $$\lambda ,\,\,\,\,{\text{N}}\left( {\lambda + 1,\,2\lambda - 2,\, - 2\lambda + 1} \right)$$
It lies on $$x+2y-2z-10=0$$
$$\eqalign{ & \therefore \lambda + 1 + 4\lambda - 4 + 4\lambda - 2 = 10 \cr & \Rightarrow 9\lambda = 15 \cr & \Rightarrow \lambda = \frac{5}{3} \cr & \therefore \,\,{\text{N}}\left( {\frac{8}{3},\,\frac{4}{3},\,\frac{{ - 7}}{3}} \right) \cr} $$