Question
If $$f\left( x \right) = x{e^{x\left( {1 - x} \right)}},$$ then $$f\left( x \right)$$ is
A.
increasing on $$\left[ { - \frac{1}{2},1} \right]$$
B.
decreasing on $$R$$
C.
increasing on $$R$$
D.
decreasing on $$\left[ { - \frac{1}{2},1} \right]$$
Answer :
increasing on $$\left[ { - \frac{1}{2},1} \right]$$
Solution :
$$\eqalign{ & f\left( x \right) = x{e^{x\left( {1 - x} \right)}} \cr & \Rightarrow f'\left( x \right) = {e^{x\left( {1 - x} \right)}} + \left( {1 - 2x} \right)x{e^{x\left( {1 - x} \right)}} \cr & = - {e^{x\left( {1 - x} \right)}} + \left( {2{x^2} - x - 1} \right) = - {e^{x\left( {1 - x} \right)}} + \left( {2x + 1} \right)\left( {x - 1} \right) \cr} $$
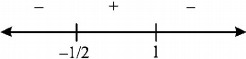
$$\therefore \,\,\,f\left( x \right)$$ is increasing on $$\left[ { - \frac{1}{2},1} \right]$$
$$\eqalign{ & f\left( x \right) = x{e^{x\left( {1 - x} \right)}} \cr & \Rightarrow f'\left( x \right) = {e^{x\left( {1 - x} \right)}} + \left( {1 - 2x} \right)x{e^{x\left( {1 - x} \right)}} \cr & = - {e^{x\left( {1 - x} \right)}} + \left( {2{x^2} - x - 1} \right) = - {e^{x\left( {1 - x} \right)}} + \left( {2x + 1} \right)\left( {x - 1} \right) \cr} $$

$$\therefore \,\,\,f\left( x \right)$$ is increasing on $$\left[ { - \frac{1}{2},1} \right]$$