Question
If center of a regular hexagon is at origin and one of the vertex on argand diagram is $$1 + 2i,$$ then its perimeter is
A.
$$2\sqrt 5 $$
B.
$$6\sqrt 2 $$
C.
$$4\sqrt 5 $$
D.
$$6\sqrt 5 $$
Answer :
$$6\sqrt 5 $$
Solution :
Let the vertices be $${z_0},{z_1},.....,{z_5}$$ w.r.t. center $$O$$ at origin and $$\left| {{z_0}} \right| = \sqrt 5 .$$
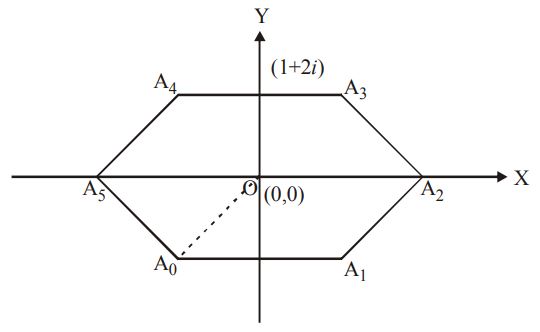
$$\eqalign{ & \Rightarrow \,{A_0}{A_1} = \left| {{z_1} - {z_0}} \right| = \left| {{z_0}{e^{i\theta }} - {z_0}} \right| \cr & = \,\left| {{z_0}} \right|\left| {\cos \,\theta + i\,\sin \,\theta - 1} \right| \cr & = \,\sqrt 5 \sqrt {{{\left( {\cos \,\theta - 1} \right)}^2} + {{\sin }^2}\,\theta } \cr & = \,\sqrt 5 \sqrt {2\left( {1 - \cos \,\theta } \right)} = \sqrt 5 \,2\sin \left( {\frac{\theta }{2}} \right) \cr & \Rightarrow \,{A_0}{A_1} = \sqrt 5 .\,2\sin \left( {\frac{\pi }{6}} \right) = \sqrt 5 \cr & \left( {\because \,\theta = \frac{{2\pi }}{6} = \frac{\pi }{3}} \right) \cr} $$
Similarly, $${A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} + {A_5}{A_0} = 6\sqrt 5 .$$
Hence the perimeter of regular polygon is
$$ = \,{A_0}{A_1} + {A_1}{A_2} + {A_2}{A_3} + {A_3}{A_4} + {A_4}{A_5} + {A_5}{A_0} = 6\sqrt 5 .$$
Let the vertices be $${z_0},{z_1},.....,{z_5}$$ w.r.t. center $$O$$ at origin and $$\left| {{z_0}} \right| = \sqrt 5 .$$

$$\eqalign{ & \Rightarrow \,{A_0}{A_1} = \left| {{z_1} - {z_0}} \right| = \left| {{z_0}{e^{i\theta }} - {z_0}} \right| \cr & = \,\left| {{z_0}} \right|\left| {\cos \,\theta + i\,\sin \,\theta - 1} \right| \cr & = \,\sqrt 5 \sqrt {{{\left( {\cos \,\theta - 1} \right)}^2} + {{\sin }^2}\,\theta } \cr & = \,\sqrt 5 \sqrt {2\left( {1 - \cos \,\theta } \right)} = \sqrt 5 \,2\sin \left( {\frac{\theta }{2}} \right) \cr & \Rightarrow \,{A_0}{A_1} = \sqrt 5 .\,2\sin \left( {\frac{\pi }{6}} \right) = \sqrt 5 \cr & \left( {\because \,\theta = \frac{{2\pi }}{6} = \frac{\pi }{3}} \right) \cr} $$
Similarly, $${A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} + {A_5}{A_0} = 6\sqrt 5 .$$
Hence the perimeter of regular polygon is
$$ = \,{A_0}{A_1} + {A_1}{A_2} + {A_2}{A_3} + {A_3}{A_4} + {A_4}{A_5} + {A_5}{A_0} = 6\sqrt 5 .$$