Question
If $$a \in R$$ and the equation $$ - 3{\left( {x - \left[ x \right]} \right)^2} + 2\left( {x - \left[ x \right]} \right) + {a^2} = 0$$ (where $$\left[ x \right]$$ denotes the greatest integer $$ \leqslant x$$ ) has no integral solution, then all possible values of a lie in the interval:
A.
$$\left( { - 2, - 1} \right)$$
B.
$$\left( { - \infty , - 2} \right) \cup \left( {2,\infty } \right)$$
C.
$$\left( { - 1,0} \right) \cup \left( {0,1} \right)$$
D.
$$\left( {1,2} \right)$$
Answer :
$$\left( { - 1,0} \right) \cup \left( {0,1} \right)$$
Solution :
Consider $$ - 3{\left( {x - \left[ x \right]} \right)^2} + 2\left( {x - \left[ x \right]} \right) + {a^2} = 0\,$$
$$\eqalign{ & \Rightarrow \,3{\left\{ x \right\}^2} - 2\left\{ x \right\} - {a^2} = 0\,\,\,\,\,\,\,\left( {\because \,x - \left[ x \right] = \left\{ x \right\}} \right) \cr & \Rightarrow \,\,3\left( {{{\left\{ x \right\}}^2} - \frac{2}{3}\left\{ x \right\}} \right) = {a^2},a \ne 0 \cr & \Rightarrow \,\,{a^2} = 3\left\{ x \right\}\left( {\left\{ x \right\} - \frac{2}{3}} \right) \cr} $$
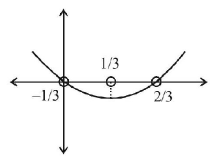
$${\text{Now,}}\,\,\left\{ x \right\} \in \left( {0,1} \right)\,\,{\text{and }}\frac{{ - 2}}{3} \leqslant {a^2} < 1\,\,\,\,\left( {{\text{by graph}}} \right)$$
Since, $$x$$ is not an integer
$$\eqalign{ & \therefore \,\,a \in \left( { - 1,1} \right) - \left\{ 0 \right\} \cr & \Rightarrow \,\,a \in \left( { - 1,0} \right) \cup \left( {0,1} \right) \cr} $$
Consider $$ - 3{\left( {x - \left[ x \right]} \right)^2} + 2\left( {x - \left[ x \right]} \right) + {a^2} = 0\,$$
$$\eqalign{ & \Rightarrow \,3{\left\{ x \right\}^2} - 2\left\{ x \right\} - {a^2} = 0\,\,\,\,\,\,\,\left( {\because \,x - \left[ x \right] = \left\{ x \right\}} \right) \cr & \Rightarrow \,\,3\left( {{{\left\{ x \right\}}^2} - \frac{2}{3}\left\{ x \right\}} \right) = {a^2},a \ne 0 \cr & \Rightarrow \,\,{a^2} = 3\left\{ x \right\}\left( {\left\{ x \right\} - \frac{2}{3}} \right) \cr} $$

$${\text{Now,}}\,\,\left\{ x \right\} \in \left( {0,1} \right)\,\,{\text{and }}\frac{{ - 2}}{3} \leqslant {a^2} < 1\,\,\,\,\left( {{\text{by graph}}} \right)$$
Since, $$x$$ is not an integer
$$\eqalign{ & \therefore \,\,a \in \left( { - 1,1} \right) - \left\{ 0 \right\} \cr & \Rightarrow \,\,a \in \left( { - 1,0} \right) \cup \left( {0,1} \right) \cr} $$