If a circle passes through the points of intersection of the lines $$2x - y + 1 = 0$$    and $$x + \lambda y - 3 = 0$$    with the axes of reference then the value of $$\lambda $$ is :

Solution :

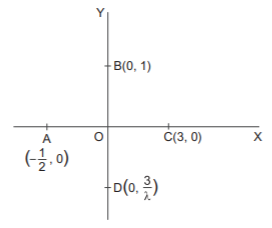
The points of intersection of $$2x - y + 1 = 0$$    with the axes are $$\left( { - \frac{1}{2},\,0} \right)$$  and $$\left( {0,\,1} \right).$$
The points of intersection of $$x + \lambda y - 3 = 0$$    and the axes are $$\left( {3,\,0} \right),\,\left( {0,\,\frac{3}{\lambda }} \right).$$
The points are concyclic if $$OA.OC = OB.OD$$
$$ \Rightarrow \frac{1}{2}.3 = 1.\left| {\frac{3}{\lambda }} \right|{\text{ or }}\left| \lambda \right| = 2$$
As $$\lambda $$ must be negative according to the geometrical situation, $$\lambda = - 2.$$