Question
If $$a, b, c$$ and $$u, v, w$$ are complex numbers representing the vertices of two triangles such that $$c = \left( {1 - r} \right)a + rb\,\,{\text{and }}w = \left( {1 - r} \right)u + rv,$$ where $$r$$ is a complex number, then the two triangles
A.
have the same area
B.
are similar
C.
are congruent
D.
none of these
Answer :
are similar
Solution :
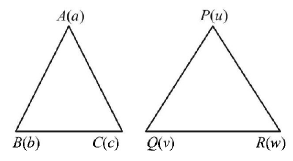
Let $$ABC$$ be the $$\Delta $$ with vertices $$a, b, c$$ and $$PQR$$ be the $$\Delta $$ with vertices $$u, v, w.$$
Then $$c = (1 - r)a + rb$$
$$\eqalign{ & \Rightarrow \,\,c - a = r\left( {b - a} \right) \cr & \Rightarrow \,\,\frac{{c - a}}{{b - a}} = r\,\,\,\,\,......\left( 1 \right) \cr & \Rightarrow \,\,w = \left( {1 - r} \right)u + rv \cr & \Rightarrow \,\,\frac{{w - u}}{{v - u}} = r\,\,\,\,......\left( 2 \right) \cr} $$
From (1) and (2) $$\left| {\frac{{c - a}}{{b - a}}} \right| = \left| {\frac{{w - u}}{{v - u}}} \right|\,\,{\text{and}}$$
$$\eqalign{ & {\text{arg}}\left( {\frac{{c - a}}{{b - a}}} \right) = {\text{arg}}\left( {\frac{{w - u}}{{v - u}}} \right) \cr & \Rightarrow \,\,\frac{{AC}}{{AB}} = \frac{{PR}}{{PQ}}\,\,{\text{and }}\angle CAB = \angle RPQ \cr & \Rightarrow \,\,\Delta ABC \sim \Delta PQR \cr} $$
Let $$ABC$$ be the $$\Delta $$ with vertices $$a, b, c$$ and $$PQR$$ be the $$\Delta $$ with vertices $$u, v, w.$$
Then $$c = (1 - r)a + rb$$

$$\eqalign{ & \Rightarrow \,\,c - a = r\left( {b - a} \right) \cr & \Rightarrow \,\,\frac{{c - a}}{{b - a}} = r\,\,\,\,\,......\left( 1 \right) \cr & \Rightarrow \,\,w = \left( {1 - r} \right)u + rv \cr & \Rightarrow \,\,\frac{{w - u}}{{v - u}} = r\,\,\,\,......\left( 2 \right) \cr} $$
From (1) and (2) $$\left| {\frac{{c - a}}{{b - a}}} \right| = \left| {\frac{{w - u}}{{v - u}}} \right|\,\,{\text{and}}$$
$$\eqalign{ & {\text{arg}}\left( {\frac{{c - a}}{{b - a}}} \right) = {\text{arg}}\left( {\frac{{w - u}}{{v - u}}} \right) \cr & \Rightarrow \,\,\frac{{AC}}{{AB}} = \frac{{PR}}{{PQ}}\,\,{\text{and }}\angle CAB = \angle RPQ \cr & \Rightarrow \,\,\Delta ABC \sim \Delta PQR \cr} $$