Question
If $$\overrightarrow a .\overrightarrow b = 0$$ and $$\overrightarrow a + \overrightarrow b $$ makes an angle of $${60^ \circ }$$ with $$\overrightarrow a ,$$ then :
A.
$$\left| {\overrightarrow a } \right| = 2\left| {\overrightarrow b } \right|$$
B.
$$2\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|$$
C.
$$\left| {\overrightarrow a } \right| = \sqrt 3 \left| {\overrightarrow b } \right|$$
D.
$$\left| {\overrightarrow b } \right| = \sqrt 3 \left| {\overrightarrow a } \right|$$
Answer :
$$\left| {\overrightarrow b } \right| = \sqrt 3 \left| {\overrightarrow a } \right|$$
Solution :
$$\eqalign{ & \left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow a = \left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow a } \right|\cos \,{60^ \circ } \cr & \Rightarrow \cos \,{60^ \circ } = \frac{1}{2} = \frac{{\left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow a }}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \frac{1}{2} = \frac{{{{\left| {\overrightarrow a } \right|}^2}}}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \frac{1}{2} = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow a + \overrightarrow b } \right|}}......\left( 1 \right) \cr & \left\{ {{\text{as }}\overrightarrow a .\overrightarrow b = 0,\,\overrightarrow a \bot \overrightarrow b } \right\} \cr} $$
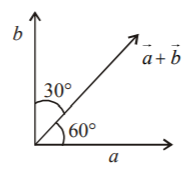
$$\eqalign{ & \left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow b = \left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow b } \right|\cos \,{30^ \circ } \cr & \Rightarrow \cos \,{30^ \circ } = \frac{{\sqrt 3 }}{2} = \frac{{\left( {\overrightarrow a + \overrightarrow b } \right).\left( {\overrightarrow b } \right)}}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow b } \right|}} \cr & \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{{{\left| {\overrightarrow b } \right|}^2}}}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow b } \right|}} \cr & \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a + \overrightarrow b } \right|}}......\left( 2 \right) \cr & {\text{Dividing}}\left( 2 \right){\text{ by}}\left( 1 \right)\,: \cr & \frac{{\frac{{\sqrt 3 }}{2}}}{{\frac{1}{2}}} = \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \sqrt 3 = \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \left| {\overrightarrow b } \right| = \sqrt 3 \left| {\overrightarrow a } \right| \cr} $$
$$\eqalign{ & \left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow a = \left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow a } \right|\cos \,{60^ \circ } \cr & \Rightarrow \cos \,{60^ \circ } = \frac{1}{2} = \frac{{\left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow a }}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \frac{1}{2} = \frac{{{{\left| {\overrightarrow a } \right|}^2}}}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \frac{1}{2} = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow a + \overrightarrow b } \right|}}......\left( 1 \right) \cr & \left\{ {{\text{as }}\overrightarrow a .\overrightarrow b = 0,\,\overrightarrow a \bot \overrightarrow b } \right\} \cr} $$

$$\eqalign{ & \left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow b = \left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow b } \right|\cos \,{30^ \circ } \cr & \Rightarrow \cos \,{30^ \circ } = \frac{{\sqrt 3 }}{2} = \frac{{\left( {\overrightarrow a + \overrightarrow b } \right).\left( {\overrightarrow b } \right)}}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow b } \right|}} \cr & \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{{{\left| {\overrightarrow b } \right|}^2}}}{{\left| {\overrightarrow a + \overrightarrow b } \right|\left| {\overrightarrow b } \right|}} \cr & \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a + \overrightarrow b } \right|}}......\left( 2 \right) \cr & {\text{Dividing}}\left( 2 \right){\text{ by}}\left( 1 \right)\,: \cr & \frac{{\frac{{\sqrt 3 }}{2}}}{{\frac{1}{2}}} = \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \sqrt 3 = \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} \cr & \Rightarrow \left| {\overrightarrow b } \right| = \sqrt 3 \left| {\overrightarrow a } \right| \cr} $$