Question
For a regular polygon, let $$r$$ and $$R$$ be the radii of the inscribed and the circumscribed circles. A false statement among the following is
A.
There is a regular polygon with $$\frac{r}{R} = \frac{1}{{\sqrt 2 }}$$
B.
There is a regular polygon with $$\frac{r}{R} = \frac{2}{3}$$
C.
There is a regular polygon with $$\frac{r}{R} = \frac{{\sqrt 3 }}{2}$$
D.
There is a regular polygon with $$\frac{r}{R} = \frac{1}{2}$$
Answer :
There is a regular polygon with $$\frac{r}{R} = \frac{2}{3}$$
Solution :
If $$O$$ is centre of polygon and $$AB$$ is one of the side, then by figure $$\cos \frac{\pi }{n} = \frac{r}{R}$$
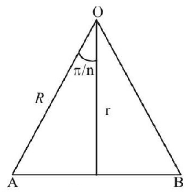
$$ \Rightarrow \,\,\frac{r}{R} = \frac{1}{2},\frac{1}{{\sqrt 2 }},\frac{{\sqrt 3 }}{2}\,\,{\text{for}}$$
$$n = 3, 4, 6$$ respectively.
If $$O$$ is centre of polygon and $$AB$$ is one of the side, then by figure $$\cos \frac{\pi }{n} = \frac{r}{R}$$

$$ \Rightarrow \,\,\frac{r}{R} = \frac{1}{2},\frac{1}{{\sqrt 2 }},\frac{{\sqrt 3 }}{2}\,\,{\text{for}}$$
$$n = 3, 4, 6$$ respectively.