Question
Each side of an equilateral triangle subtends an angle of $${60^ \circ }$$ at the top of a tower $$h\, m$$ high located at the centre of the triangle. If $$a$$ is the length of each of side of the triangle, then
A.
$$3{a^2} = 2{h^2}$$
B.
$$2{a^2} = 3{h^2}$$
C.
$${a^2} = 3{h^2}$$
D.
$$3{a^2} = {h^2}$$
Answer :
$$2{a^2} = 3{h^2}$$
Solution :
Let $$QT$$ be the tower of height $$\left( h \right)$$ in $$\Delta \,PRS.$$
Now, each triangle $$QPR, QRS, QSP$$ are equilateral.
Thus, $$QP = QS = QR = a.$$
In $$\Delta \,QTP,$$
$$\eqalign{ & Q{P^2} = Q{T^2} + P{T^2} \cr & \Rightarrow {a^2} = {h^2} + {\left( {\frac{a}{2}\sec {{30}^ \circ }} \right)^2} \cr} $$
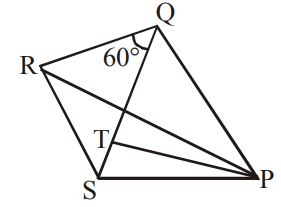
$$\eqalign{ & \Rightarrow {a^2} = {h^2} + \frac{{{a^2}}}{4} \cdot \frac{4}{3} \cr & \Rightarrow {a^2} = {h^2} + \frac{{{a^2}}}{3} \cr & \Rightarrow {a^2} - \frac{{{a^2}}}{3} = {h^2} \cr & \Rightarrow \frac{{3{a^2} - {a^2}}}{3} = {h^2} \cr & \therefore 2{a^2} = 3{h^2} \cr} $$
Let $$QT$$ be the tower of height $$\left( h \right)$$ in $$\Delta \,PRS.$$
Now, each triangle $$QPR, QRS, QSP$$ are equilateral.
Thus, $$QP = QS = QR = a.$$
In $$\Delta \,QTP,$$
$$\eqalign{ & Q{P^2} = Q{T^2} + P{T^2} \cr & \Rightarrow {a^2} = {h^2} + {\left( {\frac{a}{2}\sec {{30}^ \circ }} \right)^2} \cr} $$

$$\eqalign{ & \Rightarrow {a^2} = {h^2} + \frac{{{a^2}}}{4} \cdot \frac{4}{3} \cr & \Rightarrow {a^2} = {h^2} + \frac{{{a^2}}}{3} \cr & \Rightarrow {a^2} - \frac{{{a^2}}}{3} = {h^2} \cr & \Rightarrow \frac{{3{a^2} - {a^2}}}{3} = {h^2} \cr & \therefore 2{a^2} = 3{h^2} \cr} $$