Question
Domain of definition of the function $$f\left( x \right) = \frac{3}{{4 - {x^2}}} + {\log _{10}}\left( {{x^3} - x} \right),$$ is
A.
$$\left( { - 1,0} \right) \cup \left( {1,2} \right) \cup \left( {2,\infty } \right)$$
B.
$$\left( {a,2} \right)$$
C.
$$\left( { - 1,0} \right) \cup \left( {a,2} \right)$$
D.
$$\left( {1,2} \right) \cup \left( {2,\infty } \right).$$
Answer :
$$\left( { - 1,0} \right) \cup \left( {1,2} \right) \cup \left( {2,\infty } \right)$$
Solution :
$$\eqalign{ & f\left( x \right) = \frac{3}{{4 - {x^2}}} + {\log _{10}}\left( {{x^3} - x} \right) \cr & 4 - {x^2} \ne 0;{x^3} - x > 0 \cr & x \ne \pm \sqrt 4 {\text{ and }} - 1 < x < 0{\text{ or }}1 < x < \infty \cr} $$
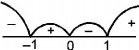
$$\eqalign{ & \therefore D = \left( { - 1,0} \right) \cup \left( {1,\infty } \right) - \left\{ {\sqrt 4 } \right\} \cr & D = \left( { - 1,0} \right) \cup \left( {1,2} \right) \cup \left( {2,\infty } \right) \cr} $$
$$\eqalign{ & f\left( x \right) = \frac{3}{{4 - {x^2}}} + {\log _{10}}\left( {{x^3} - x} \right) \cr & 4 - {x^2} \ne 0;{x^3} - x > 0 \cr & x \ne \pm \sqrt 4 {\text{ and }} - 1 < x < 0{\text{ or }}1 < x < \infty \cr} $$
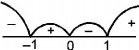
$$\eqalign{ & \therefore D = \left( { - 1,0} \right) \cup \left( {1,\infty } \right) - \left\{ {\sqrt 4 } \right\} \cr & D = \left( { - 1,0} \right) \cup \left( {1,2} \right) \cup \left( {2,\infty } \right) \cr} $$