Question
Consider the following statements :
Consider the following statements :
1. $$f\left( x \right) = \ln \,x$$ is an increasing function on $$\left( {0,\,\infty } \right)$$
2. $$f\left( x \right) = {e^x} - x\left( {\ln \,x} \right)$$ is an increasing function on $$\left( {1,\,\infty } \right).$$
Which of the above statements is/are correct ?
A.
1 only
B.
2 only
C.
Both 1 and 2
D.
Neither 1 nor 2
Answer :
Both 1 and 2
Solution :
$$\eqalign{ & f\left( x \right) = \log \,x \cr & {\text{Clearly }}f\left( x \right){\text{ is increasing on}}\,\left( {0,\,\infty } \right) \cr & f\left( x \right) = {e^x} - x\,\log \,x \cr & f'\left( x \right) = {e^x} - \left( {\log \,x + 1} \right) \cr} $$
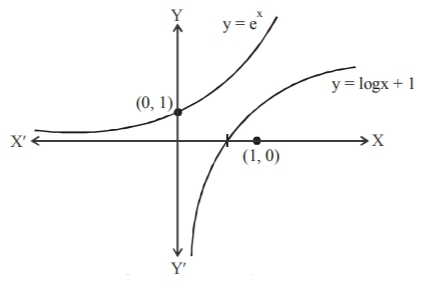
From the figure it is clear that $$f'\left( x \right) > 0$$ on $$\left( {1,\,\infty } \right).$$
So both statements (1) & (2) are correct.
$$\eqalign{ & f\left( x \right) = \log \,x \cr & {\text{Clearly }}f\left( x \right){\text{ is increasing on}}\,\left( {0,\,\infty } \right) \cr & f\left( x \right) = {e^x} - x\,\log \,x \cr & f'\left( x \right) = {e^x} - \left( {\log \,x + 1} \right) \cr} $$

From the figure it is clear that $$f'\left( x \right) > 0$$ on $$\left( {1,\,\infty } \right).$$
So both statements (1) & (2) are correct.