Question
Consider a circle with its centre lying on the focus of the parabola $${y^2} = 2px$$ such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is-
A.
$$\left( {\frac{p}{2},\,p} \right){\text{ or }}\left( {\frac{p}{2},\, - p} \right)$$
B.
$$\left( {\frac{p}{2},\, - \frac{p}{2}} \right)$$
C.
$$\left( { - \frac{p}{2},\,p} \right)$$
D.
$$\left( { - \frac{p}{2},\, - \frac{p}{2}} \right)$$
Answer :
$$\left( {\frac{p}{2},\,p} \right){\text{ or }}\left( {\frac{p}{2},\, - p} \right)$$
Solution :
The focus of parabola $${y^2} = 2px$$ is $$\left( {\frac{p}{2},\,0} \right)$$ and directrix $$x = - \frac{p}{2}$$
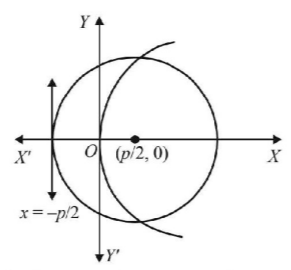
In the figure, we have supposed that $$\left. {p > 0} \right]$$
$$\therefore $$ Centre of circle is $$\left( {\frac{p}{2},\,0} \right)$$ and radius $$ = \frac{p}{2} + \frac{p}{2} = p$$
$$\therefore $$ Equation of circle is $${\left( {x - \frac{p}{2}} \right)^2} + {y^2} = {p^2}$$
For points of intersection of $${y^2} = 2px.....({\text{i}})$$
and $$4{x^2} + 4{y^2} - 4px - 3{p^2} = 0.....({\text{ii}})$$
can be obtained by solving (i) and (ii) as follows
$$\eqalign{ & 4{x^2} + 8px - 4px - 3{p^2} = 0 \cr & \Rightarrow \left( {2x + 3p} \right)\left( {2x - p} \right) = 0 \cr & \Rightarrow x = \frac{{ - 3p}}{2},\,\frac{p}{2} \cr & \Rightarrow y = - 3{p^2}\left( {{\text{not possible}}} \right),\,\,{p^2} \Rightarrow y = \pm p \cr} $$
$$\therefore $$ Required pts are $$\left( {\frac{p}{2},\,p} \right),\,\,\left( {\frac{p}{2},\, - p} \right)$$
The focus of parabola $${y^2} = 2px$$ is $$\left( {\frac{p}{2},\,0} \right)$$ and directrix $$x = - \frac{p}{2}$$

In the figure, we have supposed that $$\left. {p > 0} \right]$$
$$\therefore $$ Centre of circle is $$\left( {\frac{p}{2},\,0} \right)$$ and radius $$ = \frac{p}{2} + \frac{p}{2} = p$$
$$\therefore $$ Equation of circle is $${\left( {x - \frac{p}{2}} \right)^2} + {y^2} = {p^2}$$
For points of intersection of $${y^2} = 2px.....({\text{i}})$$
and $$4{x^2} + 4{y^2} - 4px - 3{p^2} = 0.....({\text{ii}})$$
can be obtained by solving (i) and (ii) as follows
$$\eqalign{ & 4{x^2} + 8px - 4px - 3{p^2} = 0 \cr & \Rightarrow \left( {2x + 3p} \right)\left( {2x - p} \right) = 0 \cr & \Rightarrow x = \frac{{ - 3p}}{2},\,\frac{p}{2} \cr & \Rightarrow y = - 3{p^2}\left( {{\text{not possible}}} \right),\,\,{p^2} \Rightarrow y = \pm p \cr} $$
$$\therefore $$ Required pts are $$\left( {\frac{p}{2},\,p} \right),\,\,\left( {\frac{p}{2},\, - p} \right)$$