Question
Area of the equilateral triangle inscribed in the circle $${x^2} + {y^2} - 7x + 9y + 5 = 0$$ is :
A.
$$\frac{{155}}{8}\sqrt 3 {\text{ square units}}$$
B.
$$\frac{{185}}{8}\sqrt 3 {\text{ square units}}$$
C.
$$\frac{{175}}{8}\sqrt 3 {\text{ square units}}$$
D.
$$\frac{{165}}{8}\sqrt 3 {\text{ square units}}$$
Answer :
$$\frac{{165}}{8}\sqrt 3 {\text{ square units}}$$
Solution :
Given circle : $${x^2} + {y^2} - 7x + 9y + 5 = 0$$
$$\therefore $$ Centre $$ = \left( {\frac{7}{2},\,\frac{{ - 9}}{2}} \right)$$
Radius $$ = \sqrt {\frac{{49}}{4} + \frac{{81}}{4} - 5} = \frac{{\sqrt {110} }}{2}$$
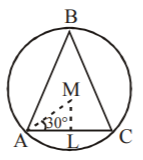
Since, $$\Delta ABC$$ is an equilateral
$$\eqalign{ & \therefore \,\angle MAL = {30^ \circ },\,\,\angle MLA = {90^ \circ } \cr & {\text{Also, }}MA = \frac{{\sqrt {110} }}{2} \cr & \therefore \,AL = MA\,\cos \,{30^ \circ } = \frac{{\sqrt {110} }}{2} \times \frac{{\sqrt 3 }}{2} = \frac{{\sqrt {330} }}{4} \cr & \therefore {\text{ side of }}\Delta = 2.AL = \frac{{\sqrt {330} }}{2} \cr} $$
Area of equilateral $$\Delta = \frac{{\sqrt 3 }}{4}{a^2} = \frac{{\sqrt 3 }}{4} \times \frac{{330}}{4} = \frac{{165}}{8}\sqrt 3 {\text{ square units}}$$
Given circle : $${x^2} + {y^2} - 7x + 9y + 5 = 0$$
$$\therefore $$ Centre $$ = \left( {\frac{7}{2},\,\frac{{ - 9}}{2}} \right)$$
Radius $$ = \sqrt {\frac{{49}}{4} + \frac{{81}}{4} - 5} = \frac{{\sqrt {110} }}{2}$$
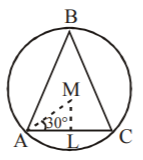
Since, $$\Delta ABC$$ is an equilateral
$$\eqalign{ & \therefore \,\angle MAL = {30^ \circ },\,\,\angle MLA = {90^ \circ } \cr & {\text{Also, }}MA = \frac{{\sqrt {110} }}{2} \cr & \therefore \,AL = MA\,\cos \,{30^ \circ } = \frac{{\sqrt {110} }}{2} \times \frac{{\sqrt 3 }}{2} = \frac{{\sqrt {330} }}{4} \cr & \therefore {\text{ side of }}\Delta = 2.AL = \frac{{\sqrt {330} }}{2} \cr} $$
Area of equilateral $$\Delta = \frac{{\sqrt 3 }}{4}{a^2} = \frac{{\sqrt 3 }}{4} \times \frac{{330}}{4} = \frac{{165}}{8}\sqrt 3 {\text{ square units}}$$