$$ABCD$$  is a square of length $$a,a \in N,a > 1.$$   Let $${L_1},{L_2},{L_3},.....$$    be points on $$BC$$  such that $$B{L_1} = {L_1}{L_2} = {L_2}{L_3} = ..... = 1$$       and $${M_1},{M_2},{M_3},.....$$    be point on $$CD$$  such that $$C{M_1} = {M_1}{M_2} = {M_2}{M_3} = ..... = 1.$$       Then $$\sum\limits_{n = 1}^{a - 1} {\left( {AL_n^2 + {L_n}M_n^2} \right)} $$    is equal to

Solution :

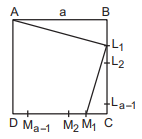
$$\eqalign{ & AL_1^2 + {L_1}M_1^2 = \left( {{a^2} + {1^2}} \right) + \left\{ {{{\left( {a - 1} \right)}^2} + {1^2}} \right\} \cr & AL_2^2 + {L_2}M_2^2 = \left( {{a^2} + {2^2}} \right) + \left\{ {{{\left( {a - 2} \right)}^2} + {2^2}} \right\} \cr & ........................................................ \cr & AL_{a - 1}^2 + {L_{a - 1}}M_{a - 1}^2 = {a^2} + {\left( {a - 1} \right)^2} + \left\{ {{1^2} + {{\left( {a - 1} \right)}^2}} \right\}. \cr} $$
∴ the required sum
$$\eqalign{ & = \left( {a - 1} \right){a^2} + \left\{ {{1^2} + {2^2} + ..... + {{\left( {a - 1} \right)}^2}} \right\} + 2\left\{ {{1^2} + {2^2} + ..... + {{\left( {a - 1} \right)}^2}} \right\} \cr & = \left( {a - 1} \right){a^2} + 3 \cdot \frac{{\left( {a - 1} \right)a\left( {2a - 1} \right)}}{6} = a\left( {a - 1} \right)\left\{ {a + \frac{{2a - 1}}{2}} \right\}. \cr} $$