Question
$$AB$$ is a vertical pole with $$B$$ at the ground level and $$A$$ at the top. A man finds that the angle of elevation of the point $$A$$ from a certain point $$C$$ on the ground is 60°. He moves away from the pole along the line $$BC$$ to a point $$D$$ such that $$CD = 7 m.$$ From $$D$$ the angle of elevation of the point $$A$$ is 45°. Then the height of the pole is
A.
$$\frac{{7\sqrt 3 }}{2}\frac{1}{{\sqrt 3 - 1}}m$$
B.
$$\frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 + 1} \right)m$$
C.
$$\frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 - 1} \right)m$$
D.
$$\frac{{7\sqrt 3 }}{2}\frac{1}{{\sqrt 3 + 1}}m$$
Answer :
$$\frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 + 1} \right)m$$
Solution :
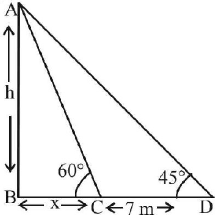
$$\eqalign{ & {\text{In }}\Delta \,ABC \cr & \frac{h}{x} = \tan {60^ \circ } = \sqrt 3 \cr & \Rightarrow \,\,x = \frac{h}{{\sqrt 3 }} \cr & {\text{In }}\Delta \,ABD\frac{h}{{x + 7}} \cr & = \tan {45^ \circ } = 1 \cr & \Rightarrow \,\,h = x + 7 \cr & \Rightarrow \,\,h - \frac{h}{{\sqrt 3 }} = 7 \cr & \Rightarrow \,\,h = \frac{{7\sqrt 3 }}{{\sqrt 3 - 1}} \times \frac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}} \cr & \Rightarrow \,\,h = \frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 + 1} \right)m \cr} $$

$$\eqalign{ & {\text{In }}\Delta \,ABC \cr & \frac{h}{x} = \tan {60^ \circ } = \sqrt 3 \cr & \Rightarrow \,\,x = \frac{h}{{\sqrt 3 }} \cr & {\text{In }}\Delta \,ABD\frac{h}{{x + 7}} \cr & = \tan {45^ \circ } = 1 \cr & \Rightarrow \,\,h = x + 7 \cr & \Rightarrow \,\,h - \frac{h}{{\sqrt 3 }} = 7 \cr & \Rightarrow \,\,h = \frac{{7\sqrt 3 }}{{\sqrt 3 - 1}} \times \frac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}} \cr & \Rightarrow \,\,h = \frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 + 1} \right)m \cr} $$