Question
A tower standing at right angles to the ground subtends an $${\sin ^{ - 1}}\frac{1}{3}$$ and $${\sin ^{ - 1}}\frac{1}{{\sqrt 5 }}$$ at two points $$A$$ and $$B$$ situated in a line through the foot of the tower and on the opposite sides. If $$AB = 50$$ units, then the height of the tower is :
A.
$$50$$
B.
$$25\sqrt 2 $$
C.
$$50\left( {\sqrt 6 - 2} \right)$$
D.
$$25\left( {\sqrt 2 - 1} \right)$$
Answer :
$$25\left( {\sqrt 2 - 1} \right)$$
Solution :
$$\eqalign{ & {\sin ^{ - 1}}\frac{1}{3} = {\cot ^{ - 1}}2\sqrt 2 \cr & {\text{and }}\,{\sin ^{ - 1}}\frac{1}{{\sqrt 5 }} = {\cot ^{ - 1}}2 \cr} $$
If $$C$$ is the foot of the tower and $$h$$ is the height, then
$$AC = h \cdot 2\sqrt 2 ,CB = h \cdot 2,h\left( {2\sqrt 2 + 2} \right) = 50$$
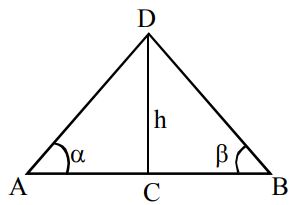
$$ \Rightarrow h = 25\left( {\sqrt 2 - 1} \right)$$
$$\eqalign{ & {\sin ^{ - 1}}\frac{1}{3} = {\cot ^{ - 1}}2\sqrt 2 \cr & {\text{and }}\,{\sin ^{ - 1}}\frac{1}{{\sqrt 5 }} = {\cot ^{ - 1}}2 \cr} $$
If $$C$$ is the foot of the tower and $$h$$ is the height, then
$$AC = h \cdot 2\sqrt 2 ,CB = h \cdot 2,h\left( {2\sqrt 2 + 2} \right) = 50$$

$$ \Rightarrow h = 25\left( {\sqrt 2 - 1} \right)$$