A stick of length $$a\,cm$$  rests against a vertical wall and the horizontal floor. If the foot of the stick slides with a constant velocity of $$b\,cm/s$$   then the magnitude of the velocity of the middle point of the stick when it is equally inclined with the floor and the wall, is :

Solution :

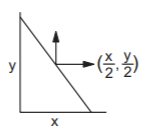
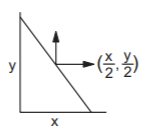
Here, $$\frac{{dx}}{{dt}} = b{\text{ cm/s,}}\,\,\,{x^2} + {y^2} = {a^2}$$
Differentiating w.r.t. $$t,\,\,2x\frac{{dx}}{{dt}} + 2y\frac{{dy}}{{dt}} = 0$$
or $$2bx + 2y\frac{{dy}}{{dt}} = 0\,\,\,\,\, \Rightarrow \frac{{dy}}{{dt}} = - \frac{{bx}}{y}$$
The velocity of the middle point at time $$t$$
$$\eqalign{ & = \sqrt {{{\left\{ {\frac{{d\left( {\frac{x}{2}} \right)}}{{dt}}} \right\}}^2} + {{\left\{ {\frac{{d\left( {\frac{y}{2}} \right)}}{{dt}}} \right\}}^2}} \cr & = \frac{1}{2}\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} \cr & = \frac{1}{2}\sqrt {{b^2} + \frac{{{b^2}{x^2}}}{{{y^2}}}} \cr} $$
When the stick is equally inclined to the wall and to the floor, $$x=y$$
$$\therefore $$ the required velocity $$ = \frac{1}{2}\sqrt {{b^2} + {b^2}} = \frac{b}{{\sqrt 2 }}$$