Question
A rectangle with sides of length $$(2m - 1)$$ and $$(2n - 1)$$ units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is
A rectangle with sides of length $$(2m - 1)$$ and $$(2n - 1)$$ units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is
A.
$${\left( {m + n - 1} \right)^2}$$
B.
$${4^{m + n - 1}}$$
C.
$${m^2}{n^2}$$
D.
$$m\left( {m + 1} \right)n\left( {n + 1} \right)$$
Answer :
$${m^2}{n^2}$$
Solution :
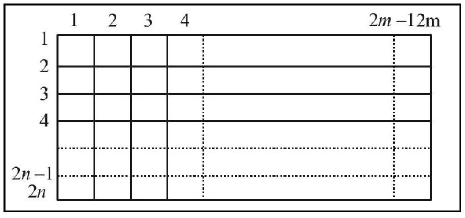
If we see the blocks in terms of lines then there are $$2m$$ vertical lines and $$2n$$ horizontal lines. To form the required rectangle we must select two horizontal lines, one even numbered (out of 2, 4, . . . . . $$2n$$) and one odd numbered (out of 1, 3, . . . . . $$2n-1$$ ) and similarly two vertical lines. The number of rectangles is
$$^m{C_1}.{\,^m}{C_1}.{\,^n}{C_1}.{\,^n}{C_1} = {m^2}{n^2}$$

If we see the blocks in terms of lines then there are $$2m$$ vertical lines and $$2n$$ horizontal lines. To form the required rectangle we must select two horizontal lines, one even numbered (out of 2, 4, . . . . . $$2n$$) and one odd numbered (out of 1, 3, . . . . . $$2n-1$$ ) and similarly two vertical lines. The number of rectangles is
$$^m{C_1}.{\,^m}{C_1}.{\,^n}{C_1}.{\,^n}{C_1} = {m^2}{n^2}$$