Question
A pole stands vertically inside a triangular park $$ABC.$$ If the angle of elevation of the top of the pole from each corner of the park is same, then the foot of the pole is at the
A.
centroid
B.
circumcentre
C.
incentre
D.
orthocentre
Answer :
centroid
Solution :
The foot of the pole is at the centroid. Because centroid is the point of intersection of medians $$AD, BE$$ and $$CF,$$ which are the lines joining a vertex with the mid point of opposite side.
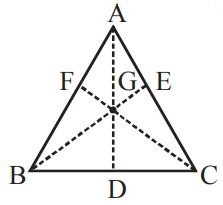
The foot of the pole is at the centroid. Because centroid is the point of intersection of medians $$AD, BE$$ and $$CF,$$ which are the lines joining a vertex with the mid point of opposite side.
