Question
A point on the hypotenuse of a triangle is at distance $$a$$ and $$b$$ from the sides of the triangle. Then the minimum length of the hypotenuse is :
A.
$${\left( {{a^{\frac{3}{2}}} + {b^{\frac{3}{2}}}} \right)^{\frac{2}{3}}}$$
B.
$${\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^{\frac{3}{2}}}$$
C.
$${\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^3}$$
D.
$${\left( {{a^{\frac{3}{2}}} + {b^{\frac{3}{2}}}} \right)^3}$$
Answer :
$${\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^{\frac{3}{2}}}$$
Solution :
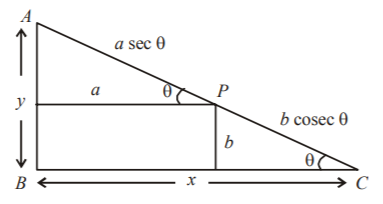
$$\eqalign{ & {\text{From the figure,}} \cr & PC = b\,{\text{cosec}}\,\theta {\text{ and }}AP = a\,\sec \,\theta \cr & AC = PC + AP \cr & {\text{or }}AC = b\,{\text{cosec}}\,\theta {\text{ }} + a\,\sec \,\theta ......\left( 1 \right) \cr & \therefore \,\frac{{d\left( {AC} \right)}}{{d\theta }} = - b\,{\text{cosec}}\,\theta \,\cot \,\theta + a\,\sec \,\theta \,\tan \,\theta \cr & {\text{For minimum length, }}\frac{{d\left( {AC} \right)}}{{d\theta }} = 0 \cr & {\text{or }}a\,\sec \,\theta \,\tan \,\theta = b\,{\text{cosec}}\,\theta \,\cot \,\theta \cr & {\text{or }}\tan \,\theta = {\left( {\frac{b}{a}} \right)^{\frac{1}{3}}} \cr & \therefore \,\,\sin \,\theta = \frac{{{{\left( b \right)}^{\frac{1}{3}}}}}{{\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}{\text{ and cos}}\,\theta = \frac{{{{\left( a \right)}^{\frac{1}{3}}}}}{{\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}.....\left( 2 \right) \cr & {\text{Also}},{\text{ }}\theta \, \in \left( {0,\,\frac{\pi }{2}} \right) \cr & \mathop {\lim }\limits_{\theta \to 0} \left( {a\,\sec \,\theta + b\,{\text{cosec}}\,\theta } \right) \to \infty \cr & {\text{Therefore, }}\theta = {\tan ^{ - 1}}{\left( {\frac{b}{a}} \right)^{\frac{1}{3}}}{\text{ is a point of minima}}{\text{.}} \cr & {\text{For this value of}}\,\theta , \cr & AC = \frac{{b\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}{{{b^{\frac{1}{3}}}}} + \frac{{a\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}{{{a^{\frac{1}{3}}}}}\,\,\,\,\,\left[ {{\text{Using }}\left( 1 \right){\text{ and }}\left( 2 \right)} \right] \cr & \,\,\,\,\,\,\,\,\,\, = \sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \left( {{b^{\frac{2}{3}}} + {a^{\frac{2}{3}}}} \right) \cr & \,\,\,\,\,\,\,\,\,\, = {\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^{\frac{3}{2}}} \cr} $$
Hence, the minimum length of the hypotenuse is $${\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^{\frac{3}{2}}}.$$

$$\eqalign{ & {\text{From the figure,}} \cr & PC = b\,{\text{cosec}}\,\theta {\text{ and }}AP = a\,\sec \,\theta \cr & AC = PC + AP \cr & {\text{or }}AC = b\,{\text{cosec}}\,\theta {\text{ }} + a\,\sec \,\theta ......\left( 1 \right) \cr & \therefore \,\frac{{d\left( {AC} \right)}}{{d\theta }} = - b\,{\text{cosec}}\,\theta \,\cot \,\theta + a\,\sec \,\theta \,\tan \,\theta \cr & {\text{For minimum length, }}\frac{{d\left( {AC} \right)}}{{d\theta }} = 0 \cr & {\text{or }}a\,\sec \,\theta \,\tan \,\theta = b\,{\text{cosec}}\,\theta \,\cot \,\theta \cr & {\text{or }}\tan \,\theta = {\left( {\frac{b}{a}} \right)^{\frac{1}{3}}} \cr & \therefore \,\,\sin \,\theta = \frac{{{{\left( b \right)}^{\frac{1}{3}}}}}{{\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}{\text{ and cos}}\,\theta = \frac{{{{\left( a \right)}^{\frac{1}{3}}}}}{{\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}.....\left( 2 \right) \cr & {\text{Also}},{\text{ }}\theta \, \in \left( {0,\,\frac{\pi }{2}} \right) \cr & \mathop {\lim }\limits_{\theta \to 0} \left( {a\,\sec \,\theta + b\,{\text{cosec}}\,\theta } \right) \to \infty \cr & {\text{Therefore, }}\theta = {\tan ^{ - 1}}{\left( {\frac{b}{a}} \right)^{\frac{1}{3}}}{\text{ is a point of minima}}{\text{.}} \cr & {\text{For this value of}}\,\theta , \cr & AC = \frac{{b\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}{{{b^{\frac{1}{3}}}}} + \frac{{a\sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} }}{{{a^{\frac{1}{3}}}}}\,\,\,\,\,\left[ {{\text{Using }}\left( 1 \right){\text{ and }}\left( 2 \right)} \right] \cr & \,\,\,\,\,\,\,\,\,\, = \sqrt {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \left( {{b^{\frac{2}{3}}} + {a^{\frac{2}{3}}}} \right) \cr & \,\,\,\,\,\,\,\,\,\, = {\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^{\frac{3}{2}}} \cr} $$
Hence, the minimum length of the hypotenuse is $${\left( {{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}} \right)^{\frac{3}{2}}}.$$