Question
A plane passes through a fixed point $$\left( {a,\,b,\,c} \right).$$ The locus of the foot of the perpendicular to it from the origin is the sphere :
A.
$${x^2} + {y^2} + {z^2} - ax - by - cz = 0$$
B.
$${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz = 0$$
C.
$${x^2} + {y^2} + {z^2} - 4ax - 4by - 4cz = 0$$
D.
None of these
Answer :
$${x^2} + {y^2} + {z^2} - ax - by - cz = 0$$
Solution :
Let $$A\left( {a,\,b,\,c} \right)$$ be the fixed point on the variable plane
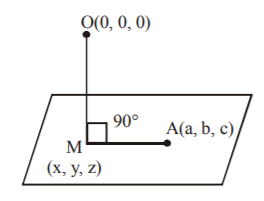
Now D.R ‘s of $$OM$$ are $$x - 0,\,y - 0,\,z - 0{\text{ i}}{\text{.e}}{\text{., }}x,\,y,\,z$$
D.R.’s of $$MA$$ are $$x - a,\,y - b,\,z - c$$
Since $$OM$$ perpendicular $$MA$$
$$\eqalign{ & x\left( {x - a} \right) + y\left( {y - b} \right) + z\left( {z - c} \right) = 0 \cr & \Rightarrow {x^2} + {y^2} + {z^2} - ax - by - cz = 0 \cr} $$
Let $$A\left( {a,\,b,\,c} \right)$$ be the fixed point on the variable plane

Now D.R ‘s of $$OM$$ are $$x - 0,\,y - 0,\,z - 0{\text{ i}}{\text{.e}}{\text{., }}x,\,y,\,z$$
D.R.’s of $$MA$$ are $$x - a,\,y - b,\,z - c$$
Since $$OM$$ perpendicular $$MA$$
$$\eqalign{ & x\left( {x - a} \right) + y\left( {y - b} \right) + z\left( {z - c} \right) = 0 \cr & \Rightarrow {x^2} + {y^2} + {z^2} - ax - by - cz = 0 \cr} $$