Question
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is $${60^ \circ }.$$ when he retreats 20 feet from the bank, he finds the angle to be $${30^ \circ }.$$ The breadth of the river in feet is :
A.
$$15$$
B.
$$15\sqrt 3 $$
C.
$$10\sqrt 3 $$
D.
$$10$$
Answer :
$$10$$
Solution :
Let $$h$$ be the height of tree $$PQ$$ and breadth of river $$PS$$ be $$x \,ft.$$
Angle of elevation subtended by a tree is $${60^ \circ }.$$
Also, when he retreats 20 feet, the angle becomes $${30^ \circ }.$$
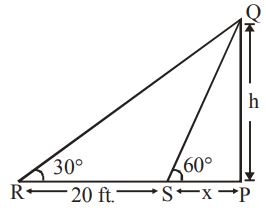
$$\eqalign{ & {\text{Also, in }}\,\Delta \,PQS,\tan {60^ \circ } = \frac{h}{x} \cr & \Rightarrow h = \sqrt 3 x \cr & {\text{and in }}\,\Delta \,PQR,\tan {30^ \circ } = \frac{h}{{x + 20}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{{x + 20}} \cr & \Rightarrow x + 20 = \sqrt 3 h \cr & \Rightarrow x + 20 = 3x\,\left( {{\text{By putting value of }}h} \right) \cr & \Rightarrow 2x = 20 \cr & \Rightarrow x = 10 \cr} $$
Hence breadth of river is $$10\,ft.$$
Let $$h$$ be the height of tree $$PQ$$ and breadth of river $$PS$$ be $$x \,ft.$$
Angle of elevation subtended by a tree is $${60^ \circ }.$$
Also, when he retreats 20 feet, the angle becomes $${30^ \circ }.$$

$$\eqalign{ & {\text{Also, in }}\,\Delta \,PQS,\tan {60^ \circ } = \frac{h}{x} \cr & \Rightarrow h = \sqrt 3 x \cr & {\text{and in }}\,\Delta \,PQR,\tan {30^ \circ } = \frac{h}{{x + 20}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{{x + 20}} \cr & \Rightarrow x + 20 = \sqrt 3 h \cr & \Rightarrow x + 20 = 3x\,\left( {{\text{By putting value of }}h} \right) \cr & \Rightarrow 2x = 20 \cr & \Rightarrow x = 10 \cr} $$
Hence breadth of river is $$10\,ft.$$