Question
A man walks a distance of 3 units from the origin towards the north-east $$\left( {N{{45}^ \circ }E} \right)$$ direction. From there, he walks a distance of 4 units towards the north-west $$\left( {N{{45}^ \circ }W} \right)$$ direction to reach a point $$P.$$ Then the position of $$P$$ in the Argand plane is
A.
$$3{e^{i\frac{\pi }{4}}} + 4i$$
B.
$$\left( {3 - 4i} \right){e^{i\frac{\pi }{4}}}$$
C.
$$\left( {4 + 3i} \right){e^{i\frac{\pi }{4}}}$$
D.
$$\left( {3 + 4i} \right){e^{i\frac{\pi }{4}}}$$
Answer :
$$\left( {3 + 4i} \right){e^{i\frac{\pi }{4}}}$$
Solution :
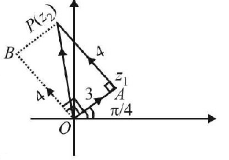
$$\eqalign{ & \overrightarrow {OP} = \overrightarrow {OA} + \overrightarrow {AP} \cr & \Rightarrow \,\,\overrightarrow {OP} = \overrightarrow {OA} + \overrightarrow {OB} \cr & \Rightarrow \,\,\overrightarrow {OP} = 3{e^{i\frac{\pi }{4}}} + 4{e^{i\left( {\frac{\pi }{2} + \frac{\pi }{4}} \right)}} \cr & = 3{e^{i\frac{\pi }{4}}} + 4{e^{i\frac{\pi }{2}}}.{e^{i\frac{\pi }{4}}} \cr & = 3{e^{i\frac{\pi }{4}}} + 4i{e^{i\frac{\pi }{4}}} = {e^{i\frac{\pi }{4}}}\left( {3 + 4i} \right). \cr} $$

$$\eqalign{ & \overrightarrow {OP} = \overrightarrow {OA} + \overrightarrow {AP} \cr & \Rightarrow \,\,\overrightarrow {OP} = \overrightarrow {OA} + \overrightarrow {OB} \cr & \Rightarrow \,\,\overrightarrow {OP} = 3{e^{i\frac{\pi }{4}}} + 4{e^{i\left( {\frac{\pi }{2} + \frac{\pi }{4}} \right)}} \cr & = 3{e^{i\frac{\pi }{4}}} + 4{e^{i\frac{\pi }{2}}}.{e^{i\frac{\pi }{4}}} \cr & = 3{e^{i\frac{\pi }{4}}} + 4i{e^{i\frac{\pi }{4}}} = {e^{i\frac{\pi }{4}}}\left( {3 + 4i} \right). \cr} $$