Question
A function $$y = f\left( x \right)$$ satisfies the condition $$f'\left( x \right)\sin \,x + f\left( x \right)\cos \,x = 1,\,f\left( x \right)$$ being bounded when $$x \to 0.$$
A function $$y = f\left( x \right)$$ satisfies the condition $$f'\left( x \right)\sin \,x + f\left( x \right)\cos \,x = 1,\,f\left( x \right)$$ being bounded when $$x \to 0.$$
If $$l = \int_0^{\frac{\pi }{2}} {f\left( x \right)dx,} $$ then :
A.
$$\frac{\pi }{2} < l < \frac{{{\pi ^2}}}{4}$$
B.
$$\frac{\pi }{4} < l < \frac{{{\pi ^2}}}{2}$$
C.
$$1 < l < \frac{\pi }{2}$$
D.
$$0 < l < 1$$
Answer :
$$\frac{\pi }{2} < l < \frac{{{\pi ^2}}}{4}$$
Solution :
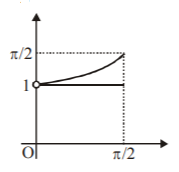
$$\eqalign{ & \sin \,x\frac{{dy}}{{dx}} + y\,\cos \,x = 1 \cr & \frac{{dy}}{{dx}} + y\,\cot \,x = {\text{cosec}}\,x \cr & {\text{I}}{\text{.F}}{\text{.}} = {e^{\int {\cot \,x\,dx} }} = {e^{\ln \left( {\sin \,x} \right)}} = \sin \,x \cr & y\,\sin \,x = \int {{\text{cosec}}\,x.\sin \,x\,dx = x + C} \cr & {\text{If }}x = 0,\,y{\text{ is finite}} \cr & \therefore \,C = 0 \cr & y = x\left( {{\text{cosec}}\,x} \right) = \frac{x}{{\sin \,x}} \cr & {\text{Now, }}l < \frac{{{\pi ^2}}}{4}{\text{ and }}l > \frac{\pi }{2} \cr & {\text{Hence, }}\frac{\pi }{2} < l < \frac{{{\pi ^2}}}{4} \cr} $$

$$\eqalign{ & \sin \,x\frac{{dy}}{{dx}} + y\,\cos \,x = 1 \cr & \frac{{dy}}{{dx}} + y\,\cot \,x = {\text{cosec}}\,x \cr & {\text{I}}{\text{.F}}{\text{.}} = {e^{\int {\cot \,x\,dx} }} = {e^{\ln \left( {\sin \,x} \right)}} = \sin \,x \cr & y\,\sin \,x = \int {{\text{cosec}}\,x.\sin \,x\,dx = x + C} \cr & {\text{If }}x = 0,\,y{\text{ is finite}} \cr & \therefore \,C = 0 \cr & y = x\left( {{\text{cosec}}\,x} \right) = \frac{x}{{\sin \,x}} \cr & {\text{Now, }}l < \frac{{{\pi ^2}}}{4}{\text{ and }}l > \frac{\pi }{2} \cr & {\text{Hence, }}\frac{\pi }{2} < l < \frac{{{\pi ^2}}}{4} \cr} $$