Question
A committee of 4 persons is to be formed from 2 ladies, 2 old men and 4 young men such that it includes at least 1 lady, at least 1 old man and at most 2 young men. Then the total number of ways in which this committee can be formed is :
A.
40
B.
41
C.
16
D.
32
Answer :
41
Solution :
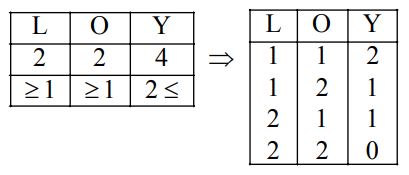
⟹
Required number of ways
$$\eqalign{ & = {\,^2}{C_1} \times {\,^2}{C_1} \times {\,^4}{C_2} \times {\,^2}{C_1} \times {\,^2}{C_2} \times {\,^4}{C_1} + {\,^2}{C_2} \times {\,^2}{C_1} \times {\,^4}{C_1} + {\,^2}{C_2} \times {\,^2}{C_2} \times {\,^4}{C_0} \cr & = 2 \times 2 \times \frac{{4 \times 3}}{2} + 2 \times 1 \times 4 + 1 \times 2 \times 4 + 1 \times 1 \times 1 \cr & = 24 + 8 + 8 + 1 = 41. \cr} $$

| L | O | Y |
| 2 | 2 | 4 |
| $$ \geqslant 1$$ | $$ \geqslant 1$$ | $$2 \leqslant $$ |
⟹
| L | O | Y |
| 1 | 1 | 2 |
| 1 | 2 | 1 |
| 2 | 1 | 1 |
| 2 | 2 | 0 |
Required number of ways
$$\eqalign{ & = {\,^2}{C_1} \times {\,^2}{C_1} \times {\,^4}{C_2} \times {\,^2}{C_1} \times {\,^2}{C_2} \times {\,^4}{C_1} + {\,^2}{C_2} \times {\,^2}{C_1} \times {\,^4}{C_1} + {\,^2}{C_2} \times {\,^2}{C_2} \times {\,^4}{C_0} \cr & = 2 \times 2 \times \frac{{4 \times 3}}{2} + 2 \times 1 \times 4 + 1 \times 2 \times 4 + 1 \times 1 \times 1 \cr & = 24 + 8 + 8 + 1 = 41. \cr} $$